Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 8
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
é a elipse .
Passo 1
E aii, pessoal!
Essa questão pede pra gente usar o Teorema de Green pra calcular uma integral de linha!
O teorema diz que se é uma curva fechada e a região dentro dessa curva, temos:
Como nossa curva é uma elipse, já sabemos que é uma curva fechada, então podemos aplicar o teorema sem problema nenhum!
Primeiro, vamos olhar pra essa região dentro da curva e definir os limites de integração. Como é uma região elíptica, faz sentido usamos coordenadas elípticas, né? Elas são assim:
Com e pra pegarmos a elipse toda, e são os seus semieixos.
Sem esquecer de multiplicar o integrando pelo jacobiano, que nesse caso é:
Definidos os limites de integração, vamos calcular , e ai transformamos nosso problema em uma integral dupla!
Passo 2
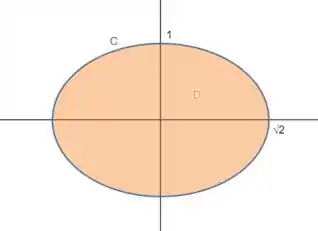
Nossa curva é definida por:
Ou
Ou seja, é uma elipse centrada na origem, de semieixo em igual a e em igual a :
Assim, a mudança de variáveis é:
Com e e .
E a integral fica:
Passo 3
Pra completar esse integrando, vamos calcular as derivadas parciais.
Nossa integral é:
Então
Derivando em função de com constante:
E em função de , mantendo constante:
Então nosso integrando fica:
Mudando para coordenadas elípticas:
E a integral fica assim:
Passo 4
Agora vamos resolver essa integral!
Vamos separar o que é função de e o que é de , e as contantes podem sair da integral:
Primeiro vamos integrar em função de , com constante:
Vamos reescrever
Então:
E fazemos a substituição
A integral fica:
Percebe que independente do quanto der a integral do , isso vai dar zero! Porque os limites de integração de são iguais!
Ou seja: