Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.6 - Ex. 13

Calcule a integral tripla.

∫ ∫ ∫ E x 2 e y   d V , onde E é delimitado pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0   ,   x = 1 e x = - 1

Passo 1

E aí, meus camaradas! Tudo em ordem?

Esse exercício pede pra gente calcular a integral tripla:

∫ ∫ ∫ E x 2 e y   d V

E é delimitado pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0   ,   x = 1 e x = - 1

Uma integral tripla em relação a V é uma integral que está buscando o volume de um sólido:

V E = ∭ E d V

Acima da região E e abaixo de uma função f .

Bom, então falta o que falta para calcularmos essa integral tripla são os limites de integração para cada variável, x , y e z .

Então nosso objetivo nessa questão é olharmos o sólido tridimensional e sua projeção no plano x y , que é a região E , para entendermos qual o limite de integração de cada variável.

Com os limites de integração em mãos, é só arranjarmos a integral na ordem que acharmos mais prático e calcular nossa integral iterada, começando da integral de dentro até a integral mais externa.

Vamo que vamo!

Passo 2

Pra gente conseguir montar a integral bonitinho, vamos primeiro visualizar um esboço da região E que é delimitada pelo cilindro parabólico z = 1 - y 2 e pelos planos z = 0   ,   x = 1 e x = - 1 , formando o sólido abaixo:

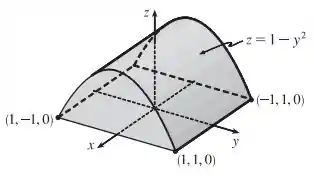
Olhando a imagem, vamos entender os limites de integração:

Para z , temos que ele varia do plano x y até a superfície z = 1 - y 2

0 ≤ y ≤ 1 - y 2

Para o eixo x , temos a variação dos valores:

- 1 ≤ x ≤ 1

Para o eixo y , temos a variação dos valores:

- 1 ≤ y ≤ 1

Então escrevemos a integral dessa forma:

∫ ∫ ∫ E x 2 e y d V = ∫ - 1 1 ∫ - 1 1 ∫ 0 1 - y 2 x 2 e y   d z   d y   d x

Uma coisa SUPER IMPORTANTE é colocarmos a integral que tem variáveis nos limites de integração por dentro da integral. Por exemplo, os limites de z são funções de y , então temos que integrar em z e só depois em y .

Passo 3

Agora vamos efetivamente calcular a integral tripla:

∫ - 1 1 ∫ - 1 1 ∫ 0 1 - y 2 x 2 e y   d z   d y   d x

Resolvendo a integral de dentro em relação a z . As demais variáveis são tratadas como constante:

∫ - 1 1 ∫ - 1 1 x 2 z e y 0 1 - y 2 d y   d x

Aplicando os limites de integração e separando a multiplicação dentro da integral em uma multiplicação de integrais:

= ∫ - 1 1 x 2   d x ∫ - 1 1 e y - y 2 e y   d y

Passo 4

Para prosseguir, precisamos do seguinte resultado, proveniente de integração por partes:

∫ y 2 e y   d y = y 2 - 2 y + 2 e y + C

Então, continuando,

∫ - 1 1 x 2   d x ∫ - 1 1 e y - y 2 e y   d y = x 3 3 - 1 1   .   e y - y 2 - 2 y + 2 e y - 1 1

Aplicando os limites de integração:

= 2 3   .   ( e - e - e - 1 + 5 e - 1 ) = 8 3 e - 1

Então, nosso resultado é:

∫ - 1 1 ∫ - 1 1 ∫ 0 1 - y 2 x 2 e y   d z   d y   d x = 8 3 e

Resposta

8 3 e

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T x d V Onde T é o tetraedro limitado pelos planos coordenados e pelo plano x + y 2 + z = 4 .
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T x y d V Onde T é a região acima do plano xy delimitada por z = 4 - x 2 ,y = 0ey = 4 .
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T d V Onde T é a região delimitada por z =x 2 + y 2 ,y + x = 2 ,x = 0 , y = 0ez = 0 .
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T x y z 2 d V Onde T é o paralelepipido retângulo 0,1×0,2 ×[ 1,3 ] .
Calcular a integral tripla dada sobre a região indicada ∫ ∫ ∫ T d V Onde T é a região do primeiro octante limitada por x=4 - y 2 ,y = z ,x = 0 ,z = 0 .