Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 15.7 - Ex. 02

Marque o ponto cujas coordenadas cilíndricas são dadas. A seguir, encontre as coordenadas retangulares do ponto.

  1. ( 1 , π ,   e )
  2. ( 1 , 3 π / 2 ,   2 )

Passo 1

  1. Como as coordenadas cilíndricas seguem o padrão ( r , θ , z ) , podemos tirar do ponto que z = e , r = 1 e θ = π então, marcando o ponto no espaço:

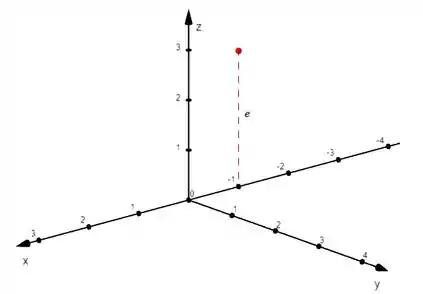
    2. Agora convertendo a coordenadas retangulares, temos que z não muda e as outras variáveis x e y seguem o modelo das coordenadas polares para a projeção do ponto no plano x y , então temos seguimos as seguintes fórmulas

    x = r cos ⁡ θ

    y = r sen ⁡ θ

    Temos que

    x = 1 cos ⁡ π = - 1

    y = 1 sen ⁡ π = 0

    z = e

    Então o ponto é ( - 1 , 0 , e ) .

    Passo 2

  2. Marcando agora o ponto ( 1,3 π / 2 ,   2 )

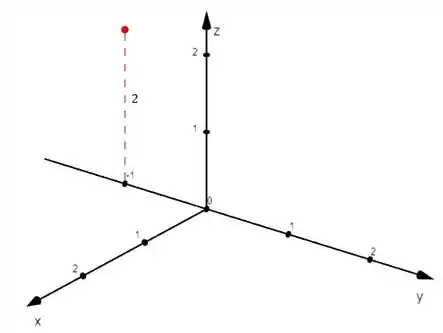
Convertendo agora as coordenadas

x = 1 cos ⁡ 3 π 2 = 0

y = 1 sen ⁡ 3 π 2 = - 1

z = 2

Então o ponto é ( 0 , - 1 , 2 ) .

Resposta

  1. ( - 1,0 , e )
  2. ( 0 , - 1,2 )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular ∭ T ( x 2 + y 2 ) d V , onde T é delimitada por x 2 + y 2 = 1 ,x 2 + y 2 = 4 ,x 2 + y 2 + z 2 = 9 e z = 0
Calcular ∭ T z . d V , onde T é a região interior às superfícies z = 0 e z = 4 - x 2 - y 2 , interior ao cilindro x 2 + y 2 = 1 .
Calcular ∭ T ( x - 2 y ) . d V , onde T é a região limitada por ( x - 1 ) 2 + ( y - 2 ) 2 = 1 , z = 0 e z = x + y .
Calcular as seguintes integrais: ∫ 0 3 ∫ 0 9 - x 2 ∫ 0 9 - x 2 - y 2 d z d y . d x
Calcular as seguintes integrais: ∫ - 1 1 ∫ - 1 - x 2 1 - x 2 ∫ x 2 + y 2 2 1 x 2 d z . d y . d x