Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.2 - Ex. 5
Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequencias de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se for convergente, calcule a soma. Se for divergente, explique o por quê.
Passo 1
E aí, galerinha! Tudo certo?
Aqui vamos começar calculando as 10 primeiras somas parciais da sequência:
No formato com até .
Depois mostraremos o gráfico tanto de (termos da sequência) quanto de (termos da série).
Através desses 10 valores e do comportamento do gráfico podemos dizer se a série parece convergir ou não, ou seja, se ela se aproxima de algum valor específico conforme seus termos crescem.
Vamos passo a passo!
Passo 2
Vamos começar calculando as somas parciais.
Para , temos:
Para :
Para :
Para :
Para :
Para :
Quase lá! Para :
Para :
Para :
Por fim, para :
UFA! Uma parte já foi!
Passo 3
Agora temos que plotar no mesmo gráfico a sequencia de termos da série e também essa sequencia das somas parciais que acabamos de achar.
Vamos só organizar numa tabelinha os resultados que vamos plotar:
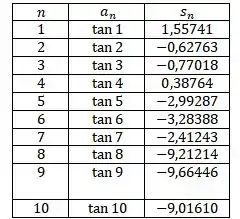
Plotando esses pontos, temos:
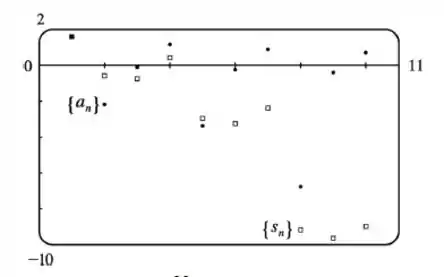
E a partir dessa figura podemos ver que a série
Diverge, já que seus termos não se aproximam de zero.
Resposta
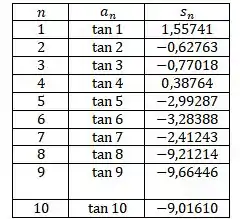
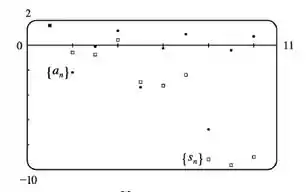
A série é divergente pois os termos não se aproximam de zero.