Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.Exercícios Práticos - Ex. 2
- A figura mostra o gráfico da velocidade (m/s) de um corpo que se desloca ao longo do eixo s durante o intervalo de t=0 a t =10 s. Qual a distância aproximada que o corpo percorreu nesses 10 segundos?
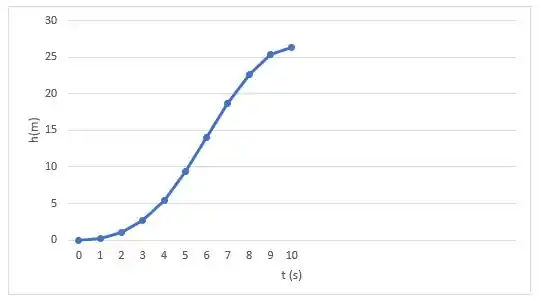
- Esboce o gráfico da altura atingida pelo foguete em função do tempo para , supondo que
Passo 1
Vamos responder o item A) primeiro, okay?
Caçando na memória, da para lembrar que a velocidade é a primeira derivada do espaço em relação ao tempo. Então nosso gráfico tá mostrando o quanto a primeira derivada da função espaço variou em relação ao tempo, beleza?
A gente sabe também que a integral é a antiderivada, então, nada mais justo calcular a integral da função derivada do tempo para obter a função espaço, certo? Porém, não foi nos dada nenhuma função, apenas o gráfico... Calma! Podemos achar o valor que o foguete atingiu como uma integral, usando a ideia de estimativas, uma forma de fazer isso é usar a regra do ponto médio. Mas para isso, vamos precisar trabalhar com cada subintervalo de tempo. Então vamos lá!
Passo 2
Olhando bem para o gráfico, conseguimos perceber que os intervalos de tempo estão divididos em (cada linha do quadradinho vale 1) e os de velocidade em 0,5 m/s cada linha do quadradinho vale 0,5). Então, podemos construir a seguinte tabela usando apenas , onde representa o início do intervalo de comprimento , representa o fim e h representa a altura. Por exemplo, no intervalo [0;0,4], olhando para o gráfico, temos que em 0, a velocidade é nula e em 0,4 é 10 pés/s, então
Passo 3
Vamos à tabela...
Passo 4
Vamos resolver o item B) .
Usando os dados da tabela do passo anterior, é só linkar cada valor de t à sua altura. Fechou?
Resposta
O espaço percorrido foi, aproximadamente, 26 metros
