Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 7.3 - Ex. 1-f

Calcule

f )   ∫ γ - y x 2 + y 2   d x + x x 2 + y 2   d y

Onde γ t   : 0,1 → R ² é uma curva C 1 por partes com imagem contida no conjunto Ω =   x , y ∈ R 2 y > 0 }   ∪ x , y ∈ R 2 x < 0 }   \   γ ( 0 ) = ( 1,1 )   e   γ ( 1 ) = (   - 1 , - 1 )      

Passo 1

Uns exercícios atrás provamos que essa função é Independente de Caminho, ou seja

∇ × F = 0  

Essa conclusão é tão forte que eu vou mostrar um método sagaz de resolver essa questão. Temos Limitações no nosso domínio. Logo Usar a função Potencial Pode ser complicado. Sugiro que façamos o seguinte

∫ A B F ⋅ d r =   ∫ t 1 t 2 F γ t ⋅ γ ' t   d t

E escolhamos um caminho fácil

Passo 2

Nossa limitações de domínio

Ω =   x , y ∈ R 2 y > 0 }   ∪ x , y ∈ R 2 x < 0 }   \   γ ( 0 ) = ( 1,1 )   e   γ ( 1 ) = (   - 1 , - 1 )      

Implicam que temos 3 quadrantes para trabalhar. Contudo O ponto (0,0) não esta no nosso domínio E também que Nosso

b = (   - 1 , - 1 )          

a = 1,1

Já que podemos escolher qualquer caminho desde que não passe pelo ponto (0,0) podemos fazer a curva abaixo

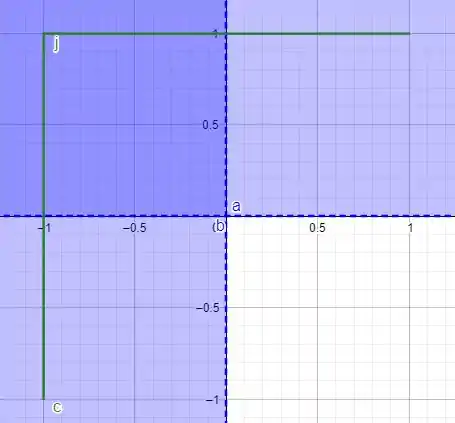
Em azul esta nosso domínio, em verde nossa curva. Vamos parametrizar assim

γ 1 =   t , 1

  γ 1 ' =   1,0

1 < t < - 1

Essa sera nossa curva horizontal. Agora a nossa curva vertical é

γ 2 = - 1 , t

γ 2 ' =   0,1

1 < t < - 1

Agora so resta aplicar

∫ t 1 t 2 F γ t ⋅ γ ' t   d t

Passo 3

Nossa função F é

F x , y =     - y x 2 + y 2   , x x 2 + y 2

Assim parametrizando fica

∫ t 1 t 2 F γ 1 t ⋅ γ 1 ' t   d t + ∫ t 1 t 2 F γ 2 t ⋅ γ 2 ' t   d t

∫ 1 - 1 F γ 1 t ⋅   1,0   d t + ∫ 1 - 1 F γ 2 t ⋅   0 , 1   d t

Sendo nossa parametrização

F γ 1 t =   - 1 t 2 + 1   ,   t t 2 + 1  

F γ 2 t = t t 2 + 1   , - 1 t 2 + 1

Agora fazendo o produto vetorial temos

∫ 1 - 1   - 1 t 2 + 1   ,   t t 2 + 1   ⋅   1,0   d t + ∫ 1 - 1 t t 2 + 1   , - 1 t 2 + 1 ⋅   0,1   d t

∫ 1 - 1 - 1 t 2 + 1     d t + ∫ 1 - 1 - 1 t 2 + 1     d t

=   - 2 ∫ 1 - 1 1 t 2 + 1     d t

Calculando essa integração nos da o seguinte resultado

= - 2   - π 2

= π

Terminamos por aqui. Te vejo na próxima resolução

: )

Resposta

∫ γ - y x 2 + y 2   d x + x x 2 + y 2   d y = π  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?d) f → x , y , z = x x 2 + y 2 + z 2 3 2 , y x 2 + y 2 + z 2 3 2 , z x 2 + y 2 + z 2 3 2 em D = x , y , z 0x 2 + y 2 + z 21
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?c) f → x , y = x x 2 + y 2 3 2 , y x 2 + y 2 3 2 em D = x , y x 2 + y 21
Verificar se os seguintes campos vetoriais são conservativos em algum domínio. Em caso afirmativo encontrar uma função potencial.b) f → = 1 + y sen ⁡ x i → + 1 - cos ⁡ x j →
Verificar se os seguintes campos vetoriais são conservativos em algum domínio. Em caso afirmativo encontrar uma função potencial.c) f → = ln ⁡ x y i → + ln ⁡ y z j → + ln ⁡ z x k →
Verificar se os seguintes campos vetoriais são conservativos em algum domínio. Em caso afirmativo encontrar uma função potencial.a) f → = 2 x i → + 5 y z j → + x 2 y 2 z 2 k →