Exercícios de Função Potencial - Lista de Exercícios Resolvida

Seja , onde é a semi-reta . Calcule

Onde é uma curva por partes, com imagem contida em , tal que e .

Decida se as afirmações abaixo são verdadeiras ou falsas, justificando. A função , onde , é um potencial para o campo , para

Encontre o trabalho realizado por sobre os caminhos de a a seguir.

1. O segmento de reta , ,
2. A hélice ,
3. O eixo de a seguido pela parábola , de a .

Mostre que os valores da integral

Não depende do caminho tomado de A a B.

Encontre uma função potencial para o campo

Determine uma função tal que sendo e use este resultado para calcular sobre a curva definida pela semicircunferência superior que começa em e termina em .

Considere a curva parametrizada por , . Calcule , onde .

Calcule a integral de linha da função vetorial ao longo da curva parametrizada por , .

22. Decida se o campo vetorial dado é conservativo. Justifique, explicitando (se for o caso) uma função potencial para .

d)

Seja . Determine o domínio do campo e mostre que é conservativo. Calcule

Determine se o campo vetorial

É conservativo. Calcule a integral de linha em que é a curva dada por

Considere o seguinte campo de vetores e seja o seu domínio de definição. Considere as seguintes afirmações:

1. é conservativo e seu domínio é simplesmente conexo
2. não é conservativo e seu domínio não é simplesmente conexo
3. admite um potencial e

Seja o campo vetorial:

Verifique se é conservativo e calcule:

Onde é a curva dada pela interseção da superfície:

Com o plano:

(Oriente de forma que a coordenada seja crescente).

Seja:

Determine as constantes e de modo que seja um campo conservativo.

Usando os valores encontrados no item anterior, calcule:

Onde é a curva parametrizada por:

Considere o seguinte campo de vetores:

E seja seu domínio de definição. Considere as seguintes afirmações:

1. é conservativo e é simplesmente conexo.
2. F não é conservativo e não é simplesmente conexo.
3. F admite um potencial e

É correto afirmar que?

Considere o campo e um parâmetro.

Seja a curva definida pela interseção da superfície com o plano , com , orientada com crescente.

Determine para o qual

11. Calcule , onde é o seguimento de extremidades e . Percorrido no sentido de para .

Considere o campo vetorial em dado por

(a) Verifique se é um campo conservativo.

(b) Se é conservativo, determine tal que .

(c) Calcule a integral de linha onde é a curva dada por

Seja uma curva parametrizada por , com

Calcule a integral de linha

Dada

1. Verificar que é um campo vetorial conservativo

Uma carga elétrica Q uniformemente distribuía ao longo de um condutor em forma de anel de raio a repele uma carga q como ao longo da linha perpendicular

]à plano do anel, através do seu centro. A magnitude da força que atua sobre a carga q quando está no ponto x é dado por

E a força aruá na direção do eixo x positivo. Encontre o trabalho realizado pela força de repulsão em mover a carga q de x=a até x=b

Sobre uma partícula que se desloca sobre o eixo x atua uma força sempre dirigida para o ponto P e cuja intensidade é igual ao inverso do quadrado da distância da partícula P

Calcule o trabalho realizado por ao deslocar a particular de até

Sejam e funções de classe arbitrárias, definidas em , e , uma curva de classe por partes, simples e fechada arbitrária. Considere as seguintes afirmações:

(I)

(II)

(III)

Assinale a alternativa verdadeira:

Escolha uma:

a) apenas a afirmação II é correta

b) todas as afirmações são verdadeiras

c) todas as afirmações são falsas

d) apenas a afirmação III é correta

e) apenas a afirmação I é correta

Um tanque de armazenamento de gasolina em forma de cilindro direito de raio 3 metros e comprimento de 12 metros está enterrado em solo em posição horizontal. Se topo do tanque estiver 4 metros abaixo da superfície, encontre o trabalho necessário para esvaziar um tanque cheio de gasolina pesando bombeando-o através de um tubo que se estende a uma altura de 2 metros acima do chão.

Seja

1. é conservativo? Por quê?
2. Calcule ,
3. Calcule , , orientada no sentido anti-horário

32) Seja qualquer curva unindo qualquer ponto na circunferência a qualquer ponto na circunferência , . Seja . Mostre que tem sempre o valor .

Questão 3: Calcule a integral de linha

Onde é a curva parametrizada com

42) Calcule

Onde e é a curva parametrizada por

Seja tal que

Se então os possíveis valores do par são:

Seja o trecho da parábola de (-1, -1) a (1,0). A integral é igual a:

Considere a hélice com

(1.1) Determine os pontos e em que a hélice acima encontra a esfera de equação

(1.2) Calcule o comprimento de arco da hélice ligando a

(1.3) Calcule a integral de linha do campo ao longo do arco ligando a .

Seja

1. seja , mostrar que é conservativo em

2. seja mostrar que é um potencial de em

3. calcular a integral de ao longo da curva para

4. seja O campo é conservativo em Justificar a respota.

40) Calcule

Onde e é a curva obtida como interseção da superfície , , e , orientada no sentido de crescimento de .

Seja o campo vetorial

1. é conservativo? Por quê?
2. Calcule , se é a curva descrita por ,
3. Calcule , onde é a fronteira do plano , que fica no primeiro octante, orientada no sentido anti-horário.

Considere o campo

a) Verifique que é conservativo e calcule tal que .

b) Seja uma superfície de nível da função , do item anterior. Calcule

onde e são dois pontos arbitrários de .

Determine se o campo vetorial

É conservativo. Calcule a integral de linha em que é a curva dada por

Calcule a integral de linha de

ao longo do caminho fechado que é fronteira da região entre os gráficos de e (orientado no sentido anti-horário). Baseado em sua resposta, diga se o campo é conservativo ou não.

Interpretando a curva , definida como onde , como sendo a função horária da posição de uma partícula , de massa , chame de a força resultante sobre .

(a) Calcule pela definição. Qual é a variação de energia cinética experimentada por ?

(b) Mostre que é um campo conservativo e calcule pelo teorema fundamental do cálculo para integrais de linha.

(c) Existe uma função escalar tal que ?

Calcule a integral de linha

Onde é o segmento de reta que liga o ponto ao ponto

Considere o campo de vetores

Onde é uma constante É claro que o domínio de é .

(3.1) Mostre que é conservativo e encontre uma função

derivável com derivadas parciais contínuas tal que

(3.2) Sejam e pontos de . Mostre que o trabalho de para mover um objeto de para depende apenas da distancia de e ao ponto .

Considere o campo de forças plano:

1. Justifique, sem calcular potenciais, se o campo é conservativo ou não.
2. Se o campo for conservativo, calcule seus potenciais.
3. . Calcule o trabalho realizado pelo campo ao deslocar uma partícula ao longo da curva

Orientada chegando à origem.

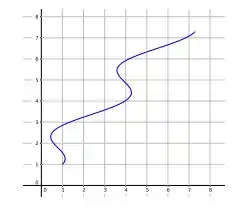
Determine o trabalho realizado pelo campo de força

ao se mover uma partícula ao longo da curva , dada por , para , mostrada abaixo.

Considere os seguintes campos:

1. Justifique, sem calcular potenciais, se os campos e são conservativos ou não.
2. Caso seja conservativo, calcule seus potenciais.
3. Seja

um campo de forças plano. Calcule o trabalho realizado por uma partícula que se desloca sobre o arco (positivamente orientado) de elipse , saindo de e chegando em

Sugestão: Relacione os campos e e use o item .

(1) Uma função potencial para o campo vetorial é:

Questão 2: Considere o campo

1. Mostre que é conservativo.
2. Calcule onde e

Seja

1. Mostre que é conservativo.
2. Calcule, onde .

Seja .

1. é conservativo? Justifique sua resposta.
2. Calcule , para a curva dada por .

Questão 2:

Seja

1. é conservativo em Justifique.
2. Calcule , onde é a circunferência percorrida uma vez no sentido anti-horário.
3. Calcule , onde é a parte da circunferência tal que , percorrida de á .