Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.4 - Ex. 3

Calcule ∫ γ x - y d x + e x + y d y , onde γ é a fronteira do trinângulo de vértice 0,0 ,   0,1 e 1,2 , orientada no sentido antí-horário.

Passo 1

A curva em questão é dada pela imagem a baixo que criamos no software Geogebra

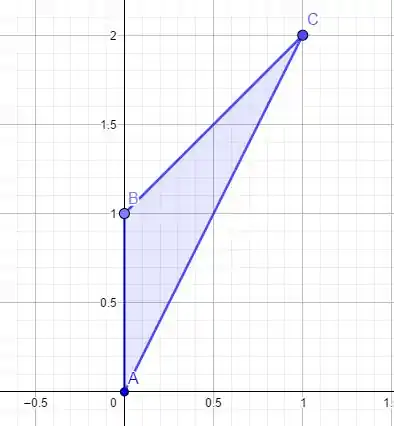
O Sentido que devemos adotar sugerido é o anti-horário, ou seja, A → C → B → A

Passo 2

Vamos fazer por partes, no caso, 3 partes. Assim

Para γ 1 A → C

γ 1 t = t , 2 t ,   0 ≤ t ≤ 1

Com

d γ 1 t = ( d t , 2 d t )

Para γ 2   C → B

γ 2 t = t , t + 1 ,   1 ≤ t ≤ 0

Com

d γ 2 t = ( d t , d t )

E para γ 3   B → A

γ 3 t = 0 , t ,   1 ≤ t ≤ 0

Com

d γ 3 t = ( 0 , d t )

Passo 3

Assim teremos que

∫ 0 1 [ - t d t + e 3 t 2 d t + ∫ 1 0 - d t + e 2 t + 1 d t + ∫ 1 0 t 0 + e t d t

Arrumando um pouquinho:

∫ 0 1 - t d t + e 3 t 2 d t + ∫ 0 1 d t - e 2 t + 1 d t - ∫ 0 1 e t d t

Que podemos resumir em

∫ 0 1 - t d t + e 3 t 2 d t + d t - e 2 t + 1 d t - e t d t

∫ 0 1 - t d t + 2 e 3 t d t + d t - e 2 t + 1 d t - e t d t

Vamos resolver agora com calma cada termo separadamente. Assim a primeira integral é dada por

∫ 0 1 - t d t = - t 2 2 0 1 = - 1 2

A segunda integral:

2 ∫ 0 1 e 3 t d t = 2 e 3 t 3 0 1 = 2 e 3 3 - 2 3

A terceira:

∫ 0 1 d t = 1

A quarta:

- ∫ 0 1 e 2 t + 1 d t = - e 2 t + 1 2 0 1 = - e 3 2 + e 2

A quinta:

- ∫ 0 1 e t d t = - e + 1

Assim o resultado final será

- 1 2 + 2 e 3 3 - 2 3 + 1 - e 3 2 + e 2 - e + 1 = e 3 6 - e 2 + 5 6

Beleza?? Acabou! 😊

Resposta

e 3 6 - e 2 + 5 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Experiências mostram que uma corrente contínua I em um fio comprido produz um campo magnético B → que é tangente a qualquer círculo em um plano perpendicular ao fio cujo centro seja o eixo do fio (com
Determine uma função f tal que F → = ∇ f e Use a parte (a) para calcular ∫ C F → ⋅ d r → sobre a curva C dada. F → x , y = x 2 i → + y 2 j → ,C é o arco da parábola y = 2 x 2 de ( - 1,2 ) a ( 2,8 )
Mostre que a integral de linha é independente e calcule a integral. ∫ C 2 x s e nyd x + ( x 2 cos ⁡ y - 3 y 2 ) d y C é qualquer caminho de ( - 1,0 ) a ( 5,1 )
Mostre que a integral de linha é independente e calcule a integral. ∫ C ( 2 y 2 - 12 x ³ y ³ )d x + ( 4 x y - 9 x 4 y 2 ) d y ³ ³ C é qualquer caminho de ( 1,1 ) a ( 3,2 )
Determine o trabalho realizado pelo campo de força F → ao mover um objeto de P a Q . F → x , y = 2 y 3 / 2 i → + 3 x y j → ;P 1,1 ,Q ( 2,4 )