Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.2 - Ex. 52
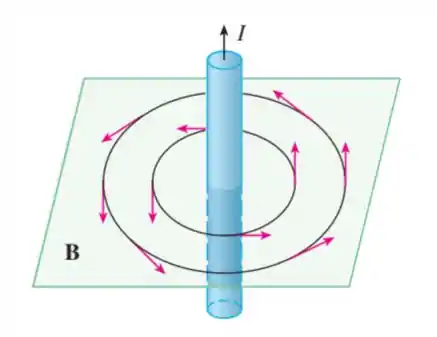
Experiências mostram que uma corrente contínua em um fio comprido produz um campo magnético que é tangente a qualquer círculo em um plano perpendicular ao fio cujo centro seja o eixo do fio (como na figura.). A Lei de Ampére relaciona a corrente elétrica ao campo magnético criado e afirma que
Onde é a corrente total que passa por qualquer superfície limitada por uma curva fechada e é uma constante chamada permeabilidade no vácuo. Tomando como um círculo de raio , mostre que o módulo de do campo magnético a uma distância do centro do fio é dado por
Passo 1
E aí, galera, tudo bem?
Essa questão é bem extensa, né? Mas não se preocupe.
O que ela quer que a gente faça é demonstrar, através da Lei de Ampére,
que o módulo de é igual ao do campo magnético a uma distância do centro do fio, que é dado por
Como estamos trabalhando com uma curva , estamos trabalhando com integrais de linhas.
Passo 2
Para esse tipo de questão, vamos primeiro parametrizar a curva , que é uma circunferência de raio :
E o vetor posição fica:
Onde o parâmetro está entre:
E o vetor ? Bom, ele é a derivada de , que está na fórmula da integral do enunciado:
Beleza!
Vamos ver agora o campo magnético! Pelo desenho vamos que as linhas de campo giram em sentido anti-horário então podemos supor que suas componentes são, por exemplo:
Passo 3
Legal! O próximo passo é fazer o produto escalar entre e (pois é o integrando da lei de Ampére!):
Passo 4
Certo! Agora já podemos colocar na integral e calcular!
E a lei de Ampére nos diz que:
Então do lado direito vamos substituir por :
E isolar :
Pronto! Era o que queríamos mostrar! 😉