Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 6.5 - Ex. 4

Calcule o momento de um fio homogêneo com a forma de uma circunferência de raio R , em torno de um diâmetro.

Passo 1

Será que vocês lembram como calcular o momento de inércia?

Eu vou ajudar vocês. Tome que o momento de inércia é definido como

I = ∫ γ r 2 d m

Onde

d m = δ x , y , z   d s

E agora devemos fazer algumas transformações para conseguimos resolvemos nosso problema.

Em nosso capítulo, Integral de linha relativa ao comprimeiro de arco, função f X contínua, definida na imagem de γ , pode ser reescrita como

∫ γ f X d s = ∫ a b f γ t | γ ' t |   d t

E será assim que podemos resolver

Passo 2

Imagine nosso fio esteja girando em torno do eixo z

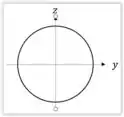
Assim podemos assumir que pitagora estava certo e que qualquer ponto dista do eixo z por

r 2 = x 2 + y 2

Outra informação que o problema dos dá é que

δ x , y , z = k = M L = M 2 π R

Assim podemos partir pra descrever nossa integral

Passo 3

Vamos fazer uma parametrização de γ t = R cos ⁡ t ,   R   s e n   t com t ∈ 0,2 π

Desta forma temos

f γ t = r γ t 2 = R 2

E

γ ' t = R

O que nos da

∫ 0 2 π k R 3 d t = 2 π k R 3

Tomando que k = M / 2 π R  

Assim temos

∫ γ f X d s = M R 2

A resposta do livro é M R 2 / 2   que é o momento de inércia em torno do eixo x , entretanto não é entorno do diâmetro.

Resposta

M R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se um arame com densidade linear ρ x ,y ,z está sobre uma curva espacial C , seus momentos de inércia em relação aos eixos x , y e z são definidos por I x = ∫ C ( y 2 + z 2 ) ρ x ,y d s I y = ∫ C ( x
Se F é o campo vetorial do Exemplo 5, mostre que ∫ C F ⋅ d r = 0 para todo caminho fechado simples que não passe pela origem e nem a circunde. F x , y = - yi + xj x 2 + y 2
Use o Exercício 22 para encontrar o centroide de um quarto de uma região circular de raio a .
Uma lâmina plana com densidade constante ρ x ,y = ρ ocupa uma região do plano x y limitada por um caminho fechado simples C . Mostre que seus momentos de inércia em relação aos eixos são I x = - ρ 3 ∮
Seja D a região limitada por um caminho fechado simples C no plano x y . Utilize o Teorema de Green para demonstrar que as coordenadas do centroide ( x - ,y - ) de D são x - = 1 2 A ∮ C x 2d y y - = -