Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.5 - Ex. 83
Calcule o valor de
por representação gráfica. Depois confirme o cálculo com a regra de L’ Hopital.
Passo 1
Para a gente determinar para onde a função vai, precisamos substituir valores bem próximos de 1 e avaliar o comportamento do gráfico.
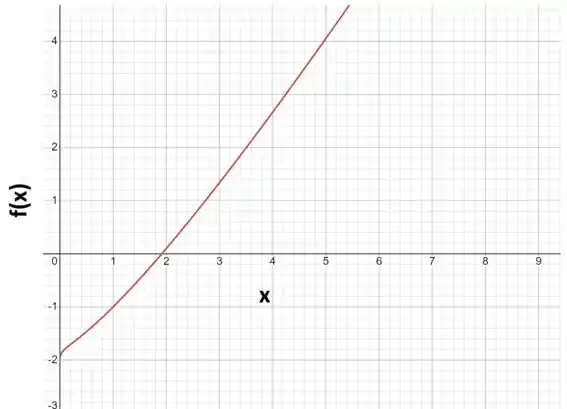
Passo 2
Olhando o gráfico a gente vê que ela vai para valores mais baixos. Então essa função vai para -1 quando x vai para 1.
Passo 3
Agora a gente vai aplicar L’ Hopital para confirmar esse reusltado!
Se substituirmos o x por 1, temos
Então a gente pode aplicar LH direto.
Passo 4
Derivando em cima e em baixo:
Passo 5
Agora podemos substituir o limite:
Resposta
Exercícios de Livros Relacionados
11 – Use a regra de l’ Hôpital para determinar o limite do exercício abaixo: lim x → ∞ 5 x 3 - 2 x 7 x 3 + 3
A regra de l'Hôpital não ajuda com os limites nos Exercícios 67-74. Tente, mas você apenas entrará em um ciclo vicioso. Determine os limites de outra forma. lim x → π 2 - sec x t gx
Use a regra de L’Hopital para determinar o seguinte exercício: l i m θ → 0 θ - s e n θ c o s θ t g θ - θ
Use a regra de L’Hopital para determinar o seguinte exercício: l i m t → 0 t ( 1 - c o s t ) t - s e n t
Use a regra de L’Hôpital para determinar o limite: lim t → 0 ts e nt1 - cos t