Calcule o volume do sólido gerado pela rotação da região infinita e o eixo x em torno do eixo x.

Lembre-se que para calcular o volume de um sólido rotacionado em relação ao eixo , temos a seguinte fórmula,

Onde R é o raio da rotação em torno do eixo

Vamos tentar encaixar nosso problema à situação acima, beleza?

Vamos tentar imaginar o solido. Veja a figura abaixo:

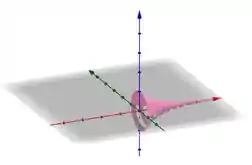
Percebe que nosso raio é a lei da própria curva? Sim?

Agora, vamos definir quem seria nossos limites de integração, beleza?

Como a rotação é infinita, então nosso limite superior tem que ser , e como nossa curva começa do este será nosso limite inferior. Então, agora é só calcular o babado, ok ? Partxiu!