Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.7 - Ex. 81
Para quais valores de a integral converge? Qual é o valor da integral quando ela converge ? Trace o gráfico do integrando para vários valores de
Passo 1
Incialmente analisaremos a integral impropria. Para isso separaremos nosso intervalo de integração de maneira conveniente em dois intervalos, ou seja,
Essa divisão foi escolhida dessa forma, pois nos exercícios 79 e 80, já analisamos os valores que deve assumir em que cada integral para que ela seja convergente.
Passo 2
No exercício 79 analisamos para quais valores de a integral
Era convergente. Sendo assim, percebermos que quando a integral convergia no intervalo de
Já, no exercício 80 analisamos para quais valores de a integral
Era convergente. Sendo assim, percebermos que quando a integral convergia no intervalo de
Passo 3
Perceba que na integral que queremos analisar, precisamos estabelecer quais valores fazem com que aquelas duas integrais sejam convergentes simultaneamente. Porém, ao analisarmos cada uma vimos que para o intervalo de , já no intervalo , isso significa que não como estabelecermos valores para de maneira que as duas integrais sejam convergentes ao mesmo tempo.
Logo,
Diverge independentemente do valor que assumir.
Plotando o gráfico de ,
Para
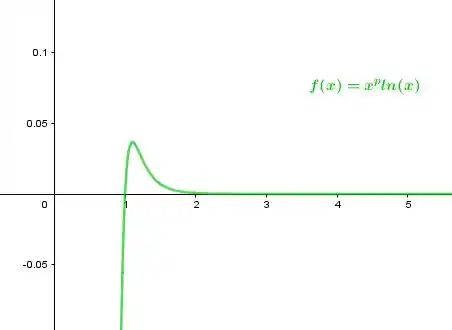
Para
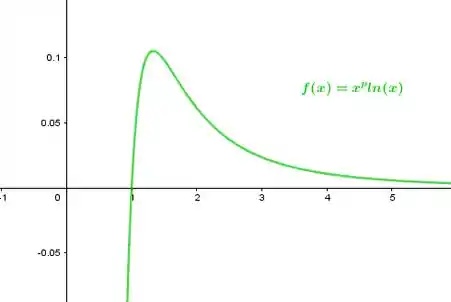
Para
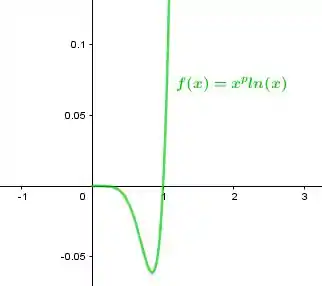
Para
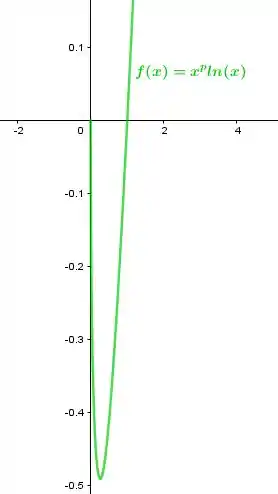
Resposta
Diverge independentemente do valor que assumir.