Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 13.2 - Ex. 2b

Calcule o volume do sólido obtido pela rotação, em torno do eixo y , do conjunto de todos os pares (x,y), tais que :

x ≤ y ≤ - x + 6   e   x ≥ 0

Passo 1

Iremos fazer dois gráficos para cada lado da inequação ( x ≤ y ≤ - x + 6 )

x ≤ y

y ≤ - x + 6  

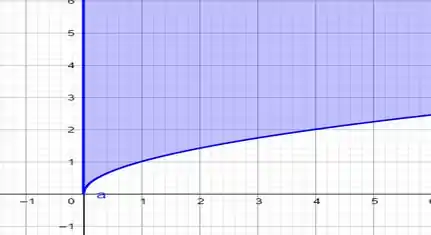
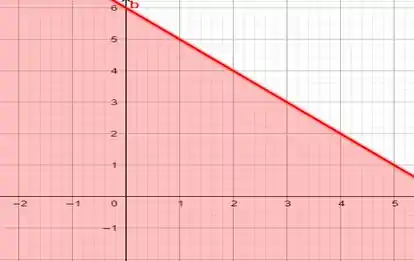
E finalmente faremos o gráfico da interseção entre os gráficos acima e x ≥ 0

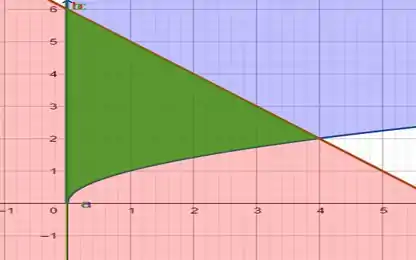
Passo 2

Vamos organizar as ideias, chamaremos de V 1 , o volume delimitado pela função y = - x + 6   e com limite de integração de 0   a   4 .

V 2 , o volume delimitado pela função   y = x ≤ y e com limite de integração de 0   a   4 .

O nosso volume será dado pela subtração entre V 1 e V 2

Caso já tenha estudado muito e esquecido, está aí a fórmula, meu amigo!!!

V = 2 π ∫ x y d x

Passo 3

Faremos o cálculo de V 1 , vem comigo!

V 1 = 2 π ∫ 0 4 - x + 6 x d x = 2 π - ∫ 0 4 x 2 d x + 6 ∫ 0 4 x d x = 2 π - x 3 3 4 0 + 3 x 2 4 0 = 2 π - 64 3 + 48 = 160 π 3

Faremos agora o cálculo de V 2 , vai tranquilo e sem afobação, continuaremos:

V 2 = 2 π ∫ 0 4 x x d x = 2 π ∫ 0 4 x 3 2 d x = 2 π 2 5 x 5 2 4 0 = 2 π 64 5 = 128 π 5

Enfim, faremos para terminar a subtração dos dois volumes calculados e dessa forma acabará o nosso sofrimento:

V = V 1 - V 2 = 160 π 3 - 128 π 5 = 800 π - 384 π 15 = 416 π 15

Resposta

V = 416 π 15

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Determine o volume do sólido obtido com a rotação da região limitada pela parábola y = x 2 e pela reta y = 1 em torno Da reta y = 1 .Da reta y = 2 .Da reta y = - 1 .
Determine o volume do sólido obtido com a rotação da região limitada pela parábola y = x 2 e pela reta y = 1 em torno Da reta y = 1 .Da reta y = 2 .Da reta y = - 1 .
Determine o volume do sólido obtido com a rotação da região limitada por y = 2 x , y = 0 e pelas retas x = 1 em torno Da reta x = 1 .Da reta x = 2 .