Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 9.4 - Ex. 34
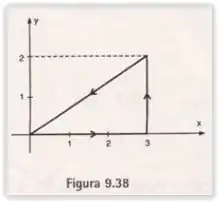
O campo de velocidade de um fluido em movimento é dado por . Calcular a circulação do fluido ao redor da curva fechada representada na Figura 9.38.
Passo 1
Precisamos inicialmente parametrizar nossas curvas afim de aplicar na equação abaixo
Onde teremos que
Passo 2
Vamos parametrizar as curvas primeiro.
Para
Para
e finalmente para
Passo 3
Agora vamos resolver nossas integrais
Assim temos que somando tudo
Resposta
Exercícios de Livros Relacionados
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(d) intersecção das superfícies z = x 2 + y 2 , x=2, do ponto A(2,0,2) a B(2,4,2 5 )
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(a) elipse x 2 4 + y 2 = 4 , z=2, uma volta completa no sentido anti-horário
15. Calcular o trabalho realizado pela força f → = 2 x + z + 4 i → + y 2 - 3 z - 1 j → + ( x - 3 y + z ) k → sobre uma partícula, ao longo de C, de A(2,4,2) a B(2,0,0), onde C é:(b) a parábola y = z 2
9. Calcular ∫ C f → ⋅ d r → , onde f → = r → r → 3 , r → = x , y , z , ao longo dos seguintes caminhos:(b) quadrado x + y = 1 ,z = 0 , no sentido anti-horário;
15. Calcular o trabalho realizado pela força f → = 2 x + z + 4 i → + y 2 - 3 z - 1 j → + ( x - 3 y + z ) k → sobre uma partícula, ao longo de C, de A(2,4,2) a B(2,0,0), onde C é:(a) o segmento de reta