Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 59

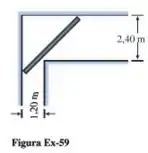
Um cano com diâmetro desprezível deve ser carregado horizontalmente em torno de um canto ligando duas passagens com e de largura (Figura Ex-59). Qual é o comprimento máximo que o cano pode ter?

Passo 1

Então pessoal, esboçando a situação que temos:

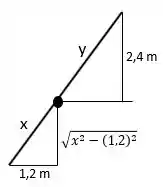
Aqui vale ressaltar que aquela raíz quadrada sai do Teorema de Pitágoras do triângulo retângulo inferior, tudo bem? Por semelhança de triângulo, tiramos:

Além disso, temos que é o comprimento do cano, que vamos chamar de . Logo:

Então encontramos uma expressão para o tamanho do cano, show!

Passo 2

Como queremos o comprimento MÁXIMO, então devemos utilizar os conceitos de cálculo que aprendemos, certo? Sendo assim, derivando nossa função:

Agora igualando a zero:

Então esse é nosso ponto crítico!

Passo 3

Substituindo o ponto crítico que encontramos na nossa função original, teremos:

E esse é nosso comprimento máximo, galera!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .c) A função f tem exatamente dois extremos relativos no intervalo I e f x → + ∞ quando x → +

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .d) A função f tem exatamente dois extremos relativos no intervalo I e f x → - ∞ quando x → +

2. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .a) f tem exatamente um extremo relativo em I e f x → 0 quando x → + ∞ e x → - ∞ .

1. Em cada parte, esboce o gráfico de uma função contínua com as propriedades indicadas, onde I = - ∞ ,+ ∞ .b) f é côncava para cima no intervalo I e não tem extremos relativos.

3. a) Use os testes da derivada primeira e da derivada segunda para mostrar que f x = 3 x 2 - 6 x + 1 tem um mínimo relativo em x = 1 .