Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.2 - Ex. 3a
3. a) Use os testes da derivada primeira e da derivada segunda para mostrar que tem um mínimo relativo em .
Passo 1
Então galera, de início o que vamos fazer é encontrar os pontos críticos da função que nos foi dada, ok? Derivando e igualando a zero, teremos:
Então só temos um ponto crítico, que é em , ok? Da derivada segunda temos:
Sendo assim, temos que a concavidade da função no intervalo em questão é para cima, o que já é um indicativo de ponto de mínimo!
Passo 2
Beleza, agora só temos que analisar como a função se comporta antes e depois do ponto crítico. Para , temos que:
Ou seja: . Para , temos que:
Ou seja: .
Se antes do ponto crítico a função é decrescente e a partir do momento em que passa pelo ponto crítico a função passa a ser crescente, então sem dúvida alguma temos um ponto de mínimo na função! Sendo assim, fica provado que, de fato, é um ponto de mínimo da função! Esboçando o gráfico para garantir:
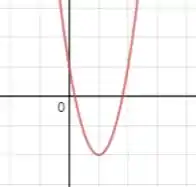
E está aí nossa prova!
Resposta
Ei, a resposta está no passo a passo :)