Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 57
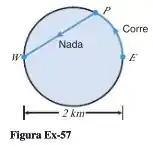
O contorno da Lagoa Circular é um círculo com diâmetro de . A rotina de treinamento de Camila começa num ponto do lado leste da lagoa. Ela corre ao longo da margem pelo norte até um ponto a partir do qual ela nada em linha reta a distância (se houver) de até o ponto diametralmente oposto a . (Figura Ex-57). Se Camila correr e nadar a , qual a distância que ela deveria correr para terminar esse percurso:
a) no menor tempo possível?
b) no maior tempo possível?
Passo 1
a) Então pessoal, antes de iniciarmos os cálculos vamos esboçar aqui a rota realizada por Camila, tudo bem? De acordo com o que o enunciado nos diz, temos o seguinte:
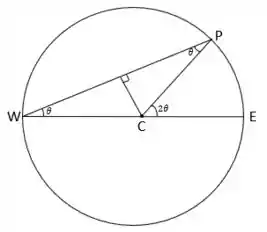
Mas de onde sai esse ângulo ? Chamamos de o ângulo , certo? De acordo com a equação do arco da circunferência, temos:
Sendo assim, temos que o ângulo será:
Substituindo o resultado:
É daí que aparece o ângulo, tudo bem? Show!
Passo 2
Assim como discutido no passo anterior, temos que a Camila corre e nada . Como , o que seria ? Do triângulo retângulo desenhado conseguimos tirar que:
Encontramos as distâncias que a Camila percorre em função do ângulo . De acordo com o que estudamos em cinemática, a velocidade média de uma partícula ou um corpo é dada da seguinte forma:
Temos as informações sobre a velocidade e sobre a distância percorrida por Camila nos dois trajetos (na corrida e na natação), logo, para a corrida teremos:
Substituindo os valores que temos:
E para a natação teremos:
Substituindo os valores que temos:
Então o tempo total será:
Vale ressaltar que e foram dados pelo enunciado, tudo bem? Então bora continuar esse trem!
Passo 3
Agora que encontramos uma expressão que define o tempo que Camila levará para terminar o trajeto, podemos determinar a distância que ela deveria correr para terminar esse percurso no menor tempo possível! Para fazermos isso basta utilizarmos os conceitos de máximos e mínimos que aprendemos! Derivando nossa função:
Aqui vale ressaltar que nosso intervalo é , pois é a validade da decomposição que fizemos no passo . Igualando nossa derivada a zero:
Logo:
Agora que encontramos nosso ponto crítico, vamos substituir esse ponto e os pontos do nosso intervalo na nossa função original para ver quando o tempo é mínimo!
Logo, podemos notar que o menor tempo ocorre quando , então a distância que minimiza será:
Ou seja, quando Camila vai direto de para , o que faz sentido, não é mesmo? 😊
Passo 4
b) De acordo com o que encontramos no passo 3, o maior tempo ocorre quando , então a distância que maximiza será:
E está aí nossa resolução, galera!
Resposta
a) Distância que minimiza o tempo: ;
b) Distância que maximiza o tempo: .