Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 74

Um cano de metal está sendo carregado através de um corredor com 3   m de largura. No fim do corredor há uma curva em ângulo reto, passando-se para um corredor com 2   m   de largura. Qual é o comprimento do cano mais longo que pode ser carregado horizontalmente em torno do canto?

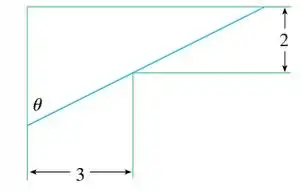
Passo 1

Opa, bora pra mais uma questão!? O enunciado nos da a seguinte situação:

“Um cano de metal está sendo carregado através de um corredor com 3   m de largura. No fim do corredor há uma curva em ângulo reto, passando-se para um corredor com 2   m   de largura.” Pra ajudar tem essa figura aqui:

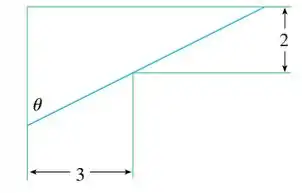
E pergunta o comprimento do cano mais longo que pode ser carregado horizontalmente em torno do canto. Precisamos montar uma função do comprimento em função de θ e depois calcular seu máximo. Vamos botar a mão na massa?

Passo 2

Podemos dividir a figura acima em dois triângulos semelhantes:

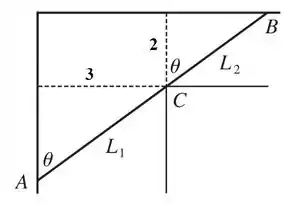
Assim teremos:

L = L 1 + L 2

sin ⁡ θ = 3 L 1

cos ⁡ θ   = 2 L 2

Substituindo:

L = 3 sin ⁡ θ + 2 cos ⁡ θ  

Ou então:

L = 3 cossec ⁡ θ + 2 sec ⁡ θ .

Passo 3

Derivando em relação a θ temos:

d L d θ = - 3 cossec ⁡ θ cot ⁡ θ   + 2 sec ⁡ θ tan ⁡ θ = 0

Igualando a zero:

- 3 cossec ⁡ θ cot ⁡ θ   + 2 sec ⁡ θ tan ⁡ θ = 0

3 cossec ⁡ θ cot ⁡ θ   = 2 sec ⁡ θ tan ⁡ θ

Simplificando:

3 sin ⁡ θ 1 tan ⁡ θ = 2 cos ⁡ θ tan ⁡ θ

tan 3 ⁡ θ = 3 2

Então:

tan ⁡ θ = 3 2 1 3

Passo 4

Queremos substituir esse resultado em:

L = 3 sin ⁡ θ + 2 cos ⁡ θ  

Podemos fazer:

tan ⁡ θ = 3 2 1 3

tan 2 ⁡ θ = 3 2 2 3

Lembrando que:

sin 2 ⁡ x + cos 2 ⁡ x = 1

Dividindo todo mundo por cos 2 ⁡ x :

tan 2 ⁡ x + 1 = 1 cos 2 ⁡ x

Logo:

1 cos 2 ⁡ θ = 3 2 2 3 + 1

De forma similar podemos fazer:

1 sin 2 ⁡ θ = 1 + 1 tan 2 ⁡ θ  

1 sin 2 ⁡ θ = 1 + 2 3 2 3 +

Substituindo em L e calculando:

L = 3 1 + 3 2 - 2 3 1 2 + 2 1 + 3 2 2 3 1 2 ≈ 21,07   m

Uhuuuul!

Resposta

O comprimento mais longo é mais ou menos 21,07   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As margens de cima e de baixo de um pôster têm 6c m , e as margens laterais medem 4c m . Se a área do material impresso sobre o pôster estiver fixa em 384c m ² ², encontre as dimensões do pôster com a
Uma cerca de 2 m de altura corre paralela a um edifício alto, a uma distância de 1 m do edifício. Qual o comprimento da menor escada que se apoie no chão e na parede do prédio, por cima da cerca?
Responde o exercício 33 se um pedaço estiver dobrado no formato de um quadrado e o outro num formato de um círculo.
Um cone com altura h está inscrito em outro cone maior com altura H , de forma que seu vértice esteja no centro da base do cone maior. Mostre que o cone interno tem seu volume máximo quando h = 1 3 H
Um pôster deve ter uma área de 900c m ² ² com uma margem de 3c m na base e nos lados, e uma margem de 5c m em cima. Que dimensões darão a maior área impressa?