Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 35
As margens de cima e de baixo de um pôster têm , e as margens laterais medem . Se a área do material impresso sobre o pôster estiver fixa em , encontre as dimensões do pôster com a menor área.
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão fala pra gente de um pôster que possui margens de cima e de baixo com , e as margens laterais com .
Queremos encontrar as dimensões ideias pra a que o pôster tenha a menor área possível, sabendo que a área do material impresso sobre ele está fixa em .
A ideia para resolver essa questão é encontrar uma expressão que modela a áreas desse pôster e depois otimizar essa área com a ajuda da derivada.
Assim, as dimensões que nos darão a informação de menor área possível são aquelas onde a derivada da área é igual a zero.
Vamos usar essa informação para desenvolver nossa solução. Vem comigo.
Passo 2
O enunciado nos diz que as margens de cima e de baixo de um pôster têm , e as margens laterais medem .
Assim, podemos fazer um esboço desse pôster da seguinte forma:
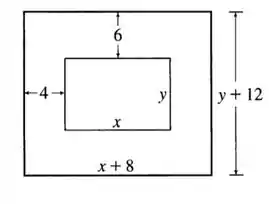
Assim, vemos que a área desse pôster pode ser expressa por:
Além disso, sabemos que a área do material impresso mede , então escrevemos:
Essa fórmula permite que a gente isole facilmente uma das variáveis, para substituirmos na primeira e fazermos a mínimização, então:
Substituindo:
E fazendo as multiplica��ões, ficamos com:
Perfeito.
Passo 3
Agora vamos procurar o valor de que faz essa área ser a menor possível usando sua derivada igual a zero.
Sendo:
Sua derivada será dada pela regra do expoente, onde:
E igualando a zero, teremos:
Passando o para o outro lado e arrumando os sinais, ficamos com:
Isolando
E extraindo sua raiz positiva, teremos:
Maravilha, já temos a dimensão , vamos agora procurar a dimensão .
Substituindo em :
E dividindo, teremos:
E prontinho.
Então, as dimensões do pôster são:
Base:
Altura:
Resposta
Dimensões mínimas do pôster:
Base:
Altura: