Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 43
Um cone com altura está inscrito em outro cone maior com altura , de forma que seu vértice esteja no centro da base do cone maior. Mostre que o cone interno tem seu volume máximo quando
Passo 1
Eaeee, belezinha?? Bom... a questão nos dá um cone com altura que está inscrito em outro cone maior com altura , de forma que seu vértice esteja no centro da base do cone maior.
Para ficar mais simples, é como se a figura nos desse essa figura:
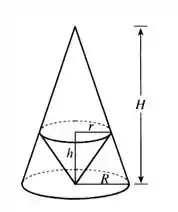
Com isso, a questão quer que provemos que que o cone interno tem seu volume máximo quando
Para isso, temos que descobrir a função responsável pelo volume do cone e maximizá-la utilizando derivadas.
Assim, lembre-se que para descobrirmos pontos de máximo ou mínimo, basta derivarmos uma função e igualar a zero!!
E aí? Bora lá aplicar?? 😉
Passo 2
No enunciado é citado o volume máximo, então a fórmula a ser maximizada é:
Também vemos no enunciado que as variáveis do cone menor estão dependendo das do cone maior, então é assim que as isolaremos, e faremos isso utilizando a nossa querida semelhança de triângulos:
Substituindo em :
Passo 3
Maximizando , ou seja, derivando e igualando a zero;
Como nesse caso é visto como uma constante, podemos dar aquela ignorada para achar .
Então:
ou
Já que não faz sentido ter um raio valendo , vamos substituir o segundo encontrado na fórmula da altura para mostrar o que o enunciado nos pede:
Então a proposição é verdade, o volume do cone realmente é máximo quando .
Resposta
Demonstração