Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 36
Um pôster deve ter uma área de com uma margem de na base e nos lados, e uma margem de em cima. Que dimensões darão a maior área impressa?
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que determinar as dimensões de um poster que maximiza a area de impressão sendo que temos de área total sendo que temos que ter uma margem na impressão de em cima e nas laterais e em baixo...
Tem ideia de como fazemos isso?
Aqui temos claramente um problema de otimização... nesses casos sempre vamos ter uma informação fixa (no caso a área total) e um dado que vamos ter que otimizar (o caso as dimensões de impressão).
Então nesse problema temos que desenvolver a equação da área em função das variáveis que queremos otimizar e tambem temos que desenvolver uma equação que relacione as variáveis que temos que otimizar.
Aí substituímos uma na outra e aplicamos a metodologia que usamos nos pontos críticos de uma função... derivamos e igualamos a .
Sacou? Bora começar!
Passo 2
Com as informações do enunciado a gente consegue fazer o seguinte desenho:
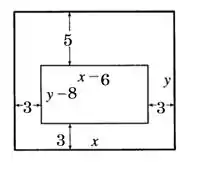
O exercício pede as dimensões da MAIOR área impressa, que tem a fórmula:
E a gente tem que a área total do pôster mede , então escrevemos:
A fórmula acima nos permite isolar uma das variáveis para substituirmos na primeira e podermos achar a área máxima, então:
Substituindo em :
Tranquilo até aqui?
Passo 3
Maximizando em função de , temos que derivar essa função e igualar a .
Manipulando essa equação para isolar , temos
Tirando a raiz nos dois lados...
Pronto, conseguimos , mas ainda falta ...
Substituindo em :
Encontramos as dimensões do poster, mas e a area impressa?
Pela imagem do passo 2, temos
Base:
Altura:
É isso! O que achou? Responde Aí!
Resposta
Dimensões da maior área impressa:
Base:
Altura: