Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.4 - Ex. 68
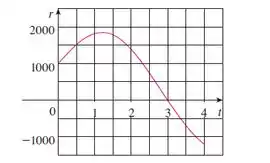
Há um fluxo de água para dentro e para fora de um tanque de armazenamento. A seguir, temos um gráfico que mostra a taxa de troca do volume de água no tanque, em litros por dia. Se a quantidade de água no tanque no instante de tempo é litros, use a Regra do Ponto Médio para estimar a quantidade de água depois de quatro dias.
Passo 1
Galera, nessa questão nós temos o fluxo de entrada ou saída de água de um tanque dado em um gráfico .
Queremos saber o quanto de água tem nesse tanque após dias sabendo que no início ele tinha um volume de
Vamos lá, pelo Teorema da Variação Total temos :
Veja bem, a questão pede a quantidade de água depois de quatro dias, então nossos limites de integração são e :
Passo 2
Temos como calcular a integral pela Regra do Ponto Médio.
A ideia aqui é basicamente dividir a nossa função em vários subintervalos. E para cada subintervalo, vamos pegar o valor da função no ponto médio do subintervalo e então calcular a área de um retângulo cuja altura é o valor da função e a base é o comprimento do subintervalo .
Como o comprimento dos subintervalos são iguais, podemos fazer:
Passo 3
Com o intervalo , e vamos usar , temos que :
Dessa forma, nossos subintervalos serão:
E substituindo os pontos médios de cada intervalo temos:
Resposta
A estimativa da quantidade de água depois de quatro dias é de litros.