Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 16.1 - Ex. 32
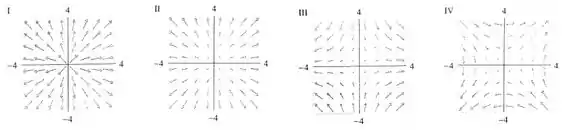
Case as funções com os desenhos de seus campos vetor gradiente.
Passo 1
Fala, galera! Tudo certo?
O exercício fornece a função e pede para dizermos qual dos gráficos representa o campo vetor gradiente. Para isso, o primeiro passo é achar o vetor gradiente:
Note que e são as derivadas parciais da nossa função em relação a cada variável. Também podemos escrever essas derivadas parciais como e .
Bem, então o que precisamos fazer aqui é, calcularmos as derivadas parciais da nossa equação e substituí-las na equação do nosso campo vetorial.
Depois vamos olhar para o formato das funções das componentes horizontais e das verticais para entendermos como deve ser o campo vetorial formado pelo nosso vetor gradiente.
Vem!
Passo 2
Vamos começar pelas derivadas parciais da nossa função:
Como temos uma função dentro da outra, aplicamos a regra da cadeia, onde multiplicamos a derivada da função com o argumento com a derivada do argumento.
Para , temos que derivar em função de , ou seja, tratando como constante:
E para , temos que derivar em função de , ou seja, tratando como constante.
Assim, nosso vetor gradiente é:
Passo 3
Agora sim podemos analisar nosso vetor e tentar entender qual seu respectivo campo vetorial:
Passando para coordenadas polares, vemos que
Assim,
Portanto, o campo deve ser radial, apontando para fora da origem e todos os vetores devem ter módulo . Os gráficos I e II apresentam campos radiais, mas apenas no I os módulos dos vetores são constantes!
Resposta
I