Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 17.3 - Ex. 14
Um circuito em série contém um resistor com , um indutor com , um capacitor e uma pilha de . A carga inicial é e a corrente inicial é .
- Determine a carga e a corrente no instante .
- Faça o gráfico das funções carga e corrente.
Passo 1
Olá, tudo bem? Vamos lá? Essa é uma questão clássica de prova! Quando um circuito está ligado em série ele pode ser descrito pela seguinte equação diferencial de segunda ordem:
Como os valores de resistência , indutância , de capacitância e de diferença de potencial , podemos montar a equação associada a esse circuito:
Passo 2
A equação diferencial de segunda ordem homogênea associada é:
E a equação característica é:
Usando a fórmula de Bháskara temos:
Aqui temos como solução duas raízes complexas e a solução da equação homogênea é dada por uma combinação linear de seno e cosseno:
Agora vamos à solução particular? Partiu?
Passo 3
A equação completa é:
Por meio do método dos coeficientes indeterminados, podemos supor uma solução particular do tipo constante:
Agora temos que derivar uma e depois mais uma vez e substituir na equação completa para determinar o valor de . Mas como tanto a derivada primeira, quanto a segunda são zero, temos:
Assim a constante é:
E a solução da equação particular associada é:
Passo 4
Agora juntando as duas soluções teremos:
Como se trata de um problema de valor inicial, podemos encontrar as constantes e .
No instante inicial a carga total é , então fazendo na solução vamos ter:
Daqui podemos tirar o valor de :
Passo 5
Agora vamos aplicar a outra condição de contorno: a corrente inicial é zero. Sabendo que corrente é a derivada temporal da carga, podemos derivas a solução em relação ao tempo:
E sabendo que temos:
Assim o sistema está totalmente definido.
A carga em função do tempo é:
E a corrente em função do tempo:
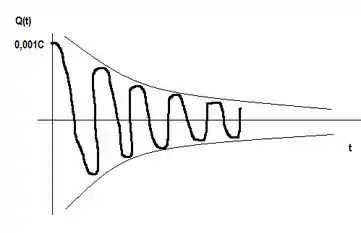
E o gráfico da carga:
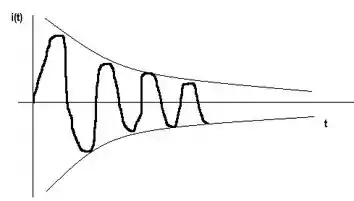
E da corrente em função do tempo:
