Combine as equações polares com os gráficos com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
- ;
- ;
Passo 1
Fala ai. Mais uma questão para analisar. E vamos começar verificando o valor da amplitude da nossa curva.
Temos que.
Para
Para
Para
Para
Para
Podemo então dizer que o valor de oscila entre e .
Vamos desenhar o gráfico de .
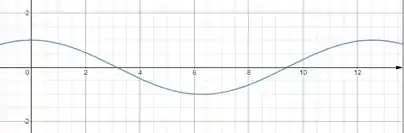
Como podemos ver, não cresce conforme aumenta, o que já nos leva a excluir os dois gráficos espirais. Além disso, não assume valores menores que , o que nos deixa com duas opções: e .
Passo 2
A função em coordenadas polares gera uma curva com um número infinito de pétalas, simétrica em relação ao eixo polar, e com um período mais curto em comparação com a função . Esta curva exibe um padrão complexo que pode ser visualizado de forma eficaz em um gráfico polar, revelando sua natureza em relação ao ângulo θ.
Sendo assim, o gráfico será:
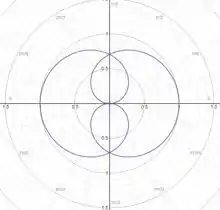
Resposta
O Gráfico correspondente é o .