Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 37
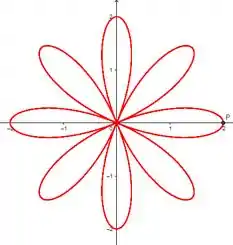
Esboce a curva com a equação dada.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Queremos esboçar esse gráfico.
Então como faremos isso???
Bom... Nessa equação não temos um termo constante, e não vai ser tão simples mudar para coordenadas cartesianas, e mesmo assim não seria uma equação que reconheceríamos como algo conhecido...
Então vamos colocar alguns valores para e substituir na equação a fim de analisarmos o seu comportamento!! 😉
Passo 2
Primeiramente calculamos valores de para alguns valores de :
Vamos calcular para :
Para :
Para :
Para :
Para :
Passo 3
Agora precisamos saber como a função se comporta entre esses ângulos, para isso vamos analisar a função .
Como o é só uma constante multiplicando, vamos analisar somente o e no gráfico dobramos todos os valores.
A análise vai ser um pouco complicada, já que temos o como multiplicativo no argumento, teremos que fazer uma análise dando voltas no círculo trigonométrico, uma volta no cosseno por quadrante do plano.
Em todos os quadrantes é como se tivéssemos dando uma volta completa, é só pensar que em uma variação de até se multiplicarmos por 4 é uma volta de à .
Portanto para todos os quadrantes o comportamento será o mesmo e o valor do cosseno vai seguir o seguinte padrão, vai começar em e então vai até , depois vai a , volta ao e por fim retorna ao .
Analisando os valores os valores negativos da função estarão sempre no centro do quadrante, então um gráfico desconsiderando esses valores seria assim:
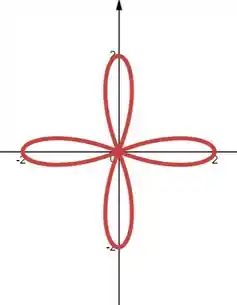
Mas se considerarmos esses valores, cada quadrante teria uma curva oposta que compensaria essa espaço do quadrante “perdido” pelo seu oposto e ficaria assim:
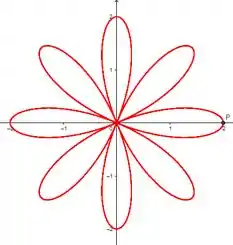
Resposta
