Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 54f
Combine as equações polares com os gráficos . Dê os motivos das suas escolhas. (Não use ferramentas gráficas.)
f)
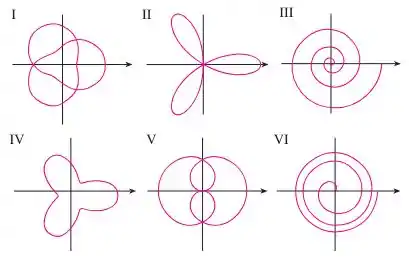
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Queremos saber qual sdos gráficos abaixo corresponde a essa equação:
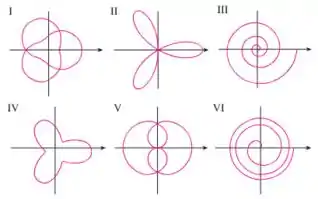
A gente não pode simplesmente colocar essa equação em um software e plotar... assim seria sem graça né? Haha
Mas e aí?? Como vamos plotar esse gráfico???
Bom... a gente pode ir construindo o gráfico na nossa cabecinha fazendo aos poucos, ou seja, analisando cada intervalo de (cada quadrante).
Agora bora lá!! 😉
Passo 2
Vamos analisar o comportamento da curva descrita no passo 2 a cada intervalo de .
Para o intervalo de para :
Ou seja, no primeiro quadrante o partiria de e iria até , veja:
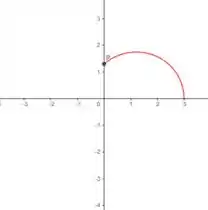
Passo 3
Para o intervalo de para :
Ou seja, no segundo quadrante o partiria de e iria até , veja:
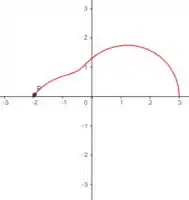
Obs: o valor é negativo por se tratar do segundo quadrante.
Passo 4
Para o intervalo de para :
Ou seja, no terceiro quadrante o partiria de e iria até , veja:
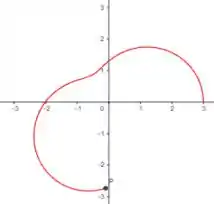
Obs: o valor é negativo por se tratarem do segundo e terceiro quadrantes.
Passo 5
Para o intervalo de para :
Ou seja, no terceiro quadrante o partiria de e iria até , veja:
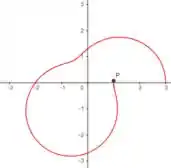
A partir daqui já podemos dizer que o gráfico será o ao final de :
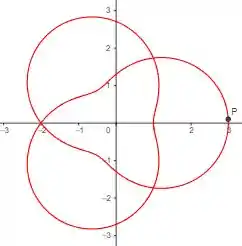
Resposta
O Gráfico correspondente é o .