Uma companhia de alta tecnologia compra um novo sistema computacional cujo valor inicial é . O sistema depreciará a uma taxa e acumulará custos de manutenção a uma taxa , onde é o tempo medido em meses. A companhia quer determinar o tempo ótimo para substituir o sistema

a) Seja

Mostre que os números críticos de ocorrem nos números nos quais .

b) Suponha que

E

Determine o período de tempo para que a depreciação total seja igual ao valor inicial

c) Determine o mínimo absoluto de em

d) Esboce os gráficos de e no mesmo sistema de coordenadas e verifique o resultado da parte (a) nesse caso

Na letra a) a questão quer que mostremos que os números críticos de ocorrem nos números nos quais

Bom... Os números críticos são os valores de tais que

Para encontrá-los, basta derivarmos a função e igualarmos a zero.

Para derivarmos, precisamos usar a regra do produto e o teorema fundamental do cálculo, daí:

Igualando a zero

Na letra b) temos as seguintes funções:

E

Com isso, queremos o período de tempo para que a depreciação total

seja igual ao valor inicial .

Assim, para , temos que a integral será

E substituindo os limites de integração, ficamos com:

Pelo enunciado, temos que

Daí

Simplificando , teremos:

E fazendo o mmc

Podemos resolver essa equação de segundo grau em sua forma fatorada com:

Assim, concluímos que

Agora que sabemos quais são as funções e , podemos calcular

E integrando, ficamos com:

E substituindo os limites de integração:

Que nos dará:

Para encontrar o valor mínimo absoluto, basta derivarmos e igualarmos a zero, daí

Igualando a zero

Sabemos que , então, aplicando o método do intervalo fechado, precisamos calcular

Ent��o, o valor de mínimo absoluto é

Esboçando os gráficos

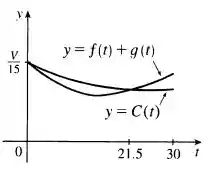
Temos que

Temos também que

Então

Que é o número crítico de .