Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 111
A extremidade vertical de um tanque de água tem de largura na borda e de profundidade, tendo a forma da região limitada pelo eixo e pelo arco da curva . Se o tanque estiver cheio de água, ache a força exercida pela pressão da água na extremidade.
Passo 1
A questão pede a força exercida sobre a extremidade de um tanque com água cujo formato é a região delimitada pela curva e o eixo .
O formato da extremidade do tanque é indicado na figura a seguir:
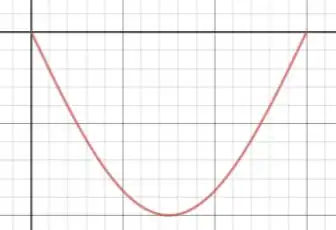
Por simplicidade, vamos adotar que o eixo aponta para baixo.
Este é um exemplo em que é muito útil usar a fórmula (4) da seção 6.7. A fórmula basicamente diz que a força é
onde é o centroide da placa. Você deve lembrar que na seção 6.5.1 definimos o centroide como
Neste caso, temos que . Assim,
Assim,
Passo 2
Para calcular essa integral, vamos fazer a substituição Assim, :
Agora você precisa lembrar que
Assim,
Fazendo a integração:
Portanto,
Desta forma,
Passo 3
Usando e , temos que