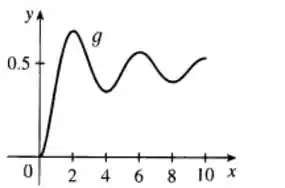
Seja
onde é a função cujo gráfico está mostrado.
- Em que valores de ocorrem os valores de máximos e mínimos locais em ?
- Onde atinge seu valor máximo absoluto?
- Em que intervalos é côncavo para baixo?
- Esboce o gráfico de .
Passo 1
Fala, galera! Tudo certinho por aí 😊?
Nessa questão, temos uma função dada como sendo uma integral definida no intervalo da seguinte forma:
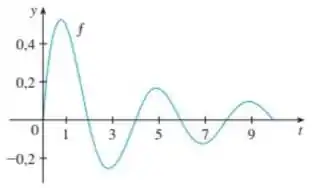
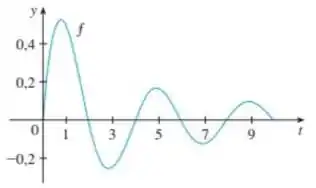
onde conhecemos apenas o gráfico da função no intervalo conforme apresetado abaixo.
Com isso, o enunciado pede para que a gente resolva os seguintes itens:
- Encontrar os pontos de máximo e mínimo locais da função .
- Dizer onde a função atinge o seu valor máximo absoluto.
- Dizer quais são os subintervalos de em que o gráfico da função é côncavo para baixo.
- Esboçar o gráfico da função .
⚠️ Presta atenção aqui!
O gráfico que conhecemos é o da função , mas os itens que precisamos responder são de características da função . Será que a gente consegue associar uma coisa com a outra?
SIM!!! Basta usarmos a Parte do Teorema Fundamental do Cálculo!
Saca só, o Teorema diz que se temos uma função
então
Ótimo! Com isso, temos que o gráfico dado também é o gráfico da derivada da função , né? Mas no que essa derivada pode nos ajudar a resolver os itens da questão 🤔?
Moleza!
- O Teste da Primeira Derivada nos diz quem se um número crítico é mínimo ou máximo local de apenas analisando o sinal da derivada ao redor dele.
- O Método do Intervalo Fechado nos diz que o valor máximo absoluto deve ser um dos máximos locais ou um dos extremos do intervalo de definição da função.
- O Teste da Concavidade nos diz sobre os intervalos de concavidade de analisado o sinal da segunda derivada
💡 Para facilitar o nosso trabalho, vamos relembrar da seguinte propriedade das integrais definidas:
- Se é um ponto no intervalo então vale que
Pronto, temos tudo o que precisamos para resolver essa questão!
Vamos lá 😊!
Passo 2
Item : Em que valores de ocorrem os valores de máximos e mínimos locais em ?
Como dito no Passo 1, pela Parte do Teorema Fundamental temos que
Logo, para encontrarmos os candidatos a mínimos e máximos locais, vamos encontrar os números críticos de , ou seja, os pontos tais que
ou não existe (mas isso não acontece aqui).
Dessa forma, analisando o gráfico de para encontrar os seus zeros, observamos que os números críticos de são
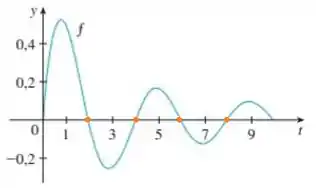
⚠️ Mas se atente ao seguinte: Os extremos do intervalo não podem ser máximo e mínimo local, né? Pois a função não está definida em ambos os lados deles.
Agora, vamos usar o Teste da Primeira Derivada nos pontos são ! Precisamos avaliar o comportamento da derivada nesses pontos, ou seja, analisar o comportamento da função (lembre-se que ) nesses pontos.
Analisando o gráfico:
- Observe que nos pontos e temos que a função muda de valores positivos para valores negativos, logo, a função também. Isso nos diz que
- Observe que nos pontos e temos que a função muda de valores negativos para valores positivos, logo, a função também. Isso nos diz que
- Observe que em temos apenas um ponto, e não uma região. Assim,
- Para observe que equivale a área da região entre a curva de e o intervalo .
- Observe que a área da região entre cada “ondinha” e o eixo é menor do que a área do retêngulo de base medindo e altura medindo o valor de no meio do intervalo.
- Observe que a área da região entre cada “ondinha” e o eixo é maior do que duas vezes a área do triângulo de base medindo 1 e altura medindo o valor de no meio do intervalo.
- Para é super fácil né, pois
- Para temos que
- Para temos que
- Para , o procedimento é análago. Temos que
- Positiva nos intervalos e
- Zero em .
- Negativa nos intervalos e
Passo 3
Intem : Onde atinge seu valor máximo absoluto?
No Passo anterior, encontramos que e são valores de máximo local, porém, na procura pelo máximo global, também precisamos considerar os extremos e .
Conseguimos responder esse item sem fazer nenhuma conta, apenas analisando o gráfico.
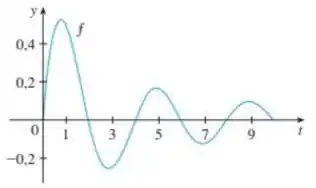
A partir de temos que a curva alterna entre valores positivos e negativos e, além disso, as “ondinhas” vão diminuindo, logo, a área da região formada por cada onda vai ficando menor, né?
Podemos pensar que o valor de é a soma das áreas da primeira e da terceira onda, subtraída da área da segunda onda, beleza?
Como o valor que é subtraído é maior do que o que é somado, temos que
Para ocorre a mesma coisa, pois é a soma de com a área da última onda, subtraída da área da penúltima onda. De novo, como o valor que é subtraído é maior do que o que é somado, temos que
Logo, vale que
Observe que o valor de é sempre não negativo Pensa assim: Da área de uma onda maior, sempre tiramos o valor da área de uma onda menor. Então, como , o máximo absoluto é
Legal, né 😊?
Agora, vamos confirmar se é isso mesmo através de estimativas para cada um desses valores? Também vamos precisar dessas estimativas para esboçar o gráfico de , no item , beleza?
Passo 4
Vamos estimar o valor de em e confirmar que o é máximo global!
Para isso, vamos limitar a área de cada ondinha por áreas de figuras geométricas simples. Saca só como:
Matematicamente, temos que para cada intervalo com vale que
Lembre-se, usamos o módulo pois a noção de área está ligada a valores positivos, porém, quando a curva de está abaixo do eixo , temos valores negativos para a integral.
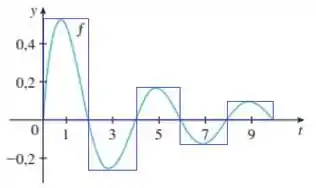
Matematicamente, temos que para cada intervalo com vale que
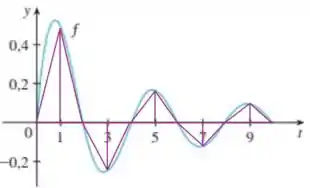
Ou seja, com essas análises temos que:
Dessa forma, uma estimativa para a área
pode ser obtida tomando o valor médio do intervalo
Logo, para cada temos que
Com isso, vamos conseguir estimar o valor de nos pontos Espia só o próximo passo!
Passo 5
Vamos estimar os valores de
nos pontos , sabendo que
para cada
Vamos usar aproximações para os valores de obtidas através do gráfico. Beleza?
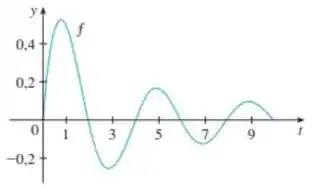
logo,
ou seja,
Como
e
então vamos ter que
ou seja
Como
e
então vamos ter que
Pronto! Estimamos o valor de nos pontos . Analisando os valores encontrados, temos que
Logo, o máximo absoluto ocorre em .
Passo 6
Intem : Em que intervalos é côncavo para baixo?
💡 Pelo Teste da Concavidade, é côncava para baixo no intervalo se para todo
Sendo assim, precisamos analisar o sinal da segunda derivada , beleza? Lembrando que , pela Parte do Teorema Fundamental, então vale que
Como a derivada representa a inclinação da reta tangente a curva de , então vamos utilizar o gráfico novamente para obter os intervalos em que
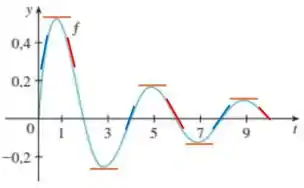
Analisando o gráfico, observamos que a inclinação da reta tangente a é:
Logo, temos que é côncava para baixo nos intervalos
Passo 3
Intem : Esboce o gráfico de .
Para construir um esboço do gráfico de , é bom nos atentarmos as seguintes informações que descobrimos:
- Os pontos de máximo local são :
- Os pontos de mínimo local são : .
- é o ponto de máximo absoluto.
- são os intervalos onde a função é côncava para baixo.
- Lembre que a função é sempre positiva.
Além disso, utilize as estimativas encontradas:
Um esboço do gráfico de é dado abaixo.
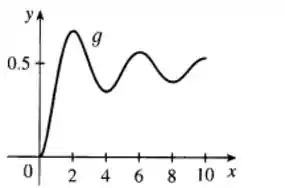
Resposta
- Os pontos de máximo local são :
- é o ponto de máximo absoluto.
- são os intervalos onde a função é côncava para baixo.
- Um esboço para o gráfico de é dado por:
Os pontos de mínimo local são : .