Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 30
Complete a demonstração do Teorema de Green demonstrando a Equação 3.
Passo 1
Fala, pessoal! Tudo tranquilo?
A questão aqui pede para demonstrarmos a Equação 3 do nosso capítulo, que é:
Podemos fazer isso resolvendo a integral dupla:
E a integral de linha:
E vemos que chegamos no mesmo resultado.
Vamos lá, então!
Passo 2
Queremos provar que
Resolvendo o lado direito como uma região do tipo II temos entre duas constantes e entre duas funções quaisquer:
Então temos, esses são nossos limites de integração pra cada variável:
Resolvendo a integral de dentro, pelo teorema fundamental do cálculo, a integral da derivada é a própria função original. Aplicando os limites de integração, ficamos só com a integral de fora:
Passo 3
Agora olhando para a integral de linha
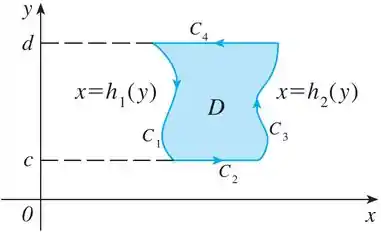
Colocando como a fronteira da região descrita , que pode ser representada graficamente como mostrado na figura a esquerda, vamos escrever e calcular a integral como soma das quatro integrais.
Para a primeira curva , como ela está com a direção para baixo, podemos parametrizar a sua negativa como como e e temos
Para as curvas e temos constante então , logo
Para podemos parametrizar como e com e temos
Então temos
Escrevendo a subtração de integrais como a integral da subtração:
Como provamos no passo anterior
E temos
Resposta
Demonstração.