Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.5 - Ex. 1d

  1. Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.

d.

∮ C x - 1 e y d x + e y ln ⁡ x + 2 x d y

C é a região limitada por

x = y 4 + 1

x = 2

Passo 1

OIii, nesse exercício vamos usar truques para resolver os nossos problemas. Na seção 6.3 tivemos que exaustivamente calcular as integrais de linha, agora temos o teorema de Green que diz

∮ C F x , y ⋅ d r = ∫ ∫ R ∇ × F d A

Outra maneira de ver isso é

∮ C F 1 d x + F 2 d y = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A  

OU seja, o trabalho do nosso campo ao percorrer a borda é igual ao fluxo que atravessa a área dentro dessa borda. O pratico do teorema de Green é que não precisamos mais procurar por parametrizações. É só calcular áreas. Então bora cair dentro!!! \o/

Passo 2

No nosso caso temos o seguinte campo

F = x - 1 e y , e y ln ⁡ x + 2 x  

Vamos então usar o teorema de Green.

∮ C F 1 d x + F 2 d y = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A  

Vamos calcular o rotacional dessa função

= ∂ F 2 ∂ x - ∂ F 1 ∂ y

= e y x + 2 - e y x

= 2  

Passo 3

Bora integrar!!!

∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

∫ ∫ R 2 d A

2 ∫ ∫ R d A

O nosso problema se resume a calcular uma área agora. Nossa região é

x = y 4 + 1

x = 2

Podemos ver graficamente abaixo

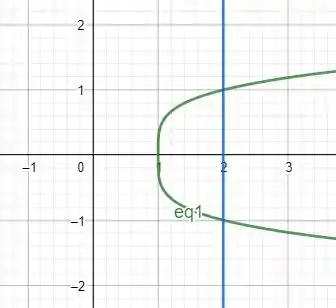
Lembrando que ao escolher nosso intervalo de integração lemos a região, da esquerda para a direita no caso do x. E de baixo para cima, no caso do y. Logo nosso intervalo de integração vai ser

x ∈ y 4 + 1 ,   2

y ∈ - 1,1

Graficamente fica fácil descobrir isso. De forma analítica teríamos que fazer um sistema com as duas equações e acharíamos

y 4 = 1

y =   ± 1

E dai vem nosso intervalo. Bora integrar

2 ∫ ∫ R d A

2 ∫ - 1 1 ∫ y 4 + 1 2 d x d y

=   2 ∫ - 1 1 2 - y 4 + 1 d y  

= 2   y - y 5 5 - 1 1

= 2   1 - - 1 - 1 5 1 5 - - 1 5

= 2   2 - 2 5

= 16 5

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

∮ C x - 1 e y d x + e y ln ⁡ x + 2 x d y = 16 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula começa na origem, se move ao longo do eixo x para o ponto ( 5,0 ) , em seguida ao longo do quarto da circunferência x 2 + y 2 = 25 ,x ≥ 0 ,y ≥ 0 para o ponto ( 0,5 ) , e então para baixo
Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla. P x , y = 2 x - x 3 y 5 , Q x , y = x 3 y 8 C é uma elipse 4 x 2 +
Verifique o Teorema de Green usando um sistema de computação algébrica para calcular tanto a integral de linha como a integral dupla. P x , y = x 3 y 4 , Q x , y = x 5 y 4 C consiste de um segmento de
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.
Calcule a integral de linha por dois métodos: a) diretamente e b) utilizando o Teorema de Green. ∮ C y d x - x d y C é o círculo com centro na origem e raio 1.