Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.5 - Ex. 1e

  1. Calcule as seguintes integrais, ao longo das curvas C , orientadas positivamente.

e.

∮ C 2 x y - x 2 d x + x - y 2 d y

C é a fronteira da região limitada por

y = x 2

y 2 = x

Passo 1

OIii, nesse exercício vamos usar truques para resolver os nossos problemas. Na seção 6.3 tivemos que exaustivamente calcular as integrais de linha, agora temos o teorema de Green que diz

∮ C F x , y ⋅ d r = ∫ ∫ R ∇ × F d A

Outra maneira de ver isso é

∮ C F 1 d x + F 2 d y = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A  

OU seja, o trabalho do nosso campo ao percorrer a borda é igual ao fluxo que atravessa a área dentro dessa borda. O pratico do teorema de Green é que não precisamos mais procurar por parametrizações. É só calcular áreas. Então bora cair dentro!!! \o/

Passo 2

No nosso caso temos o seguinte campo

F = 2 x y - x 2   ,   x - y 2  

Vamos então usar o teorema de Green.

∮ C F 1 d x + F 2 d y = ∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A  

Vamos calcular o rotacional dessa função

= ∂ F 2 ∂ x - ∂ F 1 ∂ y

= 1 - 2 x

Passo 3

Bora integrar!!!

∫ ∫ R ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

∫ ∫ R 1 - 2 x d A

Vamos encontrar nossa região

y = x 2

y 2 = x

O que graficamente obtemos

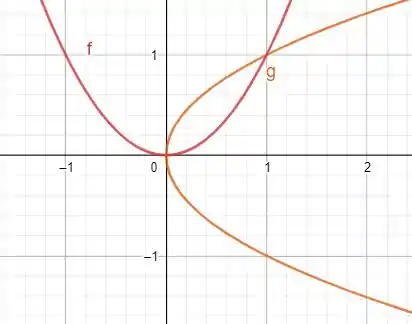
Podemos então definir o seguinte intervalo

y ∈ x 2 ,   x

x ∈ 0,1

Isso faz que na nossa integral fique da seguinte forma

∫ 0 1 ∫ x 2 x 1 - 2 x   d y d x

∫ 0 1 1 - 2 x x - x 2 d x

∫ 0 1 x 1 / 2 - 2 x 3 2 - x 2 + 2 x 3 d x

2 3 x 3 2 - 4 5 x 5 2 - x 3 3 + 2 x 4 4 0 1

= 2 3 - 4 5 - 1 3 + 1 2

= 1 30

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

∮ C 2 x y - x 2 d x + x - y 2 d y = 1 30

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x y d x + x 2 y 3 d y C é um triângulo com os vértices em 0,0 , 1,0e( 1,2 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y 2 d x + x 2 y d y C é o retângulo com os vértices em 0,0 , 5,0 , 5,4e( 0,4 ) .
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . y d x - x d y C é uma circunferência com centro na origem e r a i o = 4 .
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C x 2 + y 2 d x + x 2 - y 2 d y C é um triângulo com os vértices 0,0 , 2,1e0,1 .
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y 4 d x + 2 x y 3 d y C é a elipse x 2 + 2 y 2 = 2 .