Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.3 - Ex. 16

Comprimento da hélice O comprimento da volta da hélice no Exemplo 1 também é o comprimento da diagonal de um quadrado com unidades de lado. Mostre como obter esse quadrado cortando e aplainando uma parte do cilindro ao redor do qual a hélice gira.

Passo 1

Fala minha galera querida!! Vamos desenhar a figura do exemplo 1 para saber com o que estamos trabalhando.

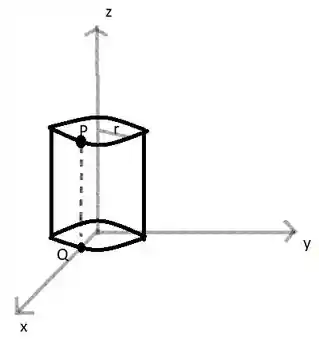
Passo 2

Bora anotar as informações que temos do enunciado para começar o exercício.

Sabemos que a hélice da uma volta completa, isto é, t vai de 0 a ;
O raio do cilindro é 1, então o comprimento da base é ;
Quando a hélice completa a volta, o ponto P está em , pois o raio é dado pela função vetorial ;
A altura do cilindro é .

Passo 3

Agora sim vamos começar o exercício, se cortarmos o cilindro da seguinte maneira,

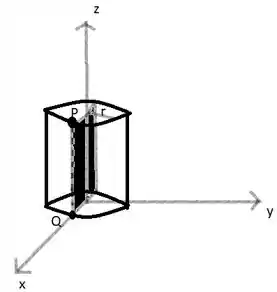
E achatar as duas partes, nós obtemos um retângulo de largura igual ao comprimento da circunferência do cilindro, e altura , a altura do cilindro.

Como a largura é igual a altura, o retângulo é um quadrado de lado .

Bora pro próximo!

Resposta

Demonstração.

Exercícios de Livros Relacionados

Distância ao longo de uma reta Mostre que, se u é um vetor unitário, então o parâmetro de comprimento de arco ao longo da reta r(t) = P 0 + tu a partir do ponto P 0 ( x 0 ,y 0 ,z 0 ) , em que t = 0, é

Comprimento de arco Encontre o comprimento da curva r t = 2 t i + 2 t j + ( 1 - t 2 ) k De (0, 0, 1) a ( 2 ,2 ,0 ) .

Nos Exercícios 11-14, encontre o parâmetro de comprimento de arco ao longo da curva a partir do ponto em que t = 0, avaliando a integral s = ∫ 0 t v τ d τ da Equação 3. Em seguida, encontre o comprime

Involuta de um círculo Se uma linha enrolada ao redor de um círculo fixo for desenrolada enquanto é mantida esticada no plano do círculo, sua extremidade P traça uma involuta do círculo. Na figura a s

Utilize a regra de Simpson com n = 10 para aproximar o comprimento do arco de r t = ti + t 2j + t 3k a partir da origem ao ponto (2, 4, 8)