Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.3 - Ex. 19
Involuta de um círculo Se uma linha enrolada ao redor de um círculo fixo for desenrolada enquanto é mantida esticada no plano do círculo, sua extremidade P traça uma involuta do círculo. Na figura a seguir, o círculo em questão é o círculo, e o ponto do traçado inicia em (1, 0). A parte desenrolada da linha é tangente ao círculo em Q, e t é a medida em radianos do ângulo a partir do eixo x positivo ao segmento OQ. Deduza as equações paramétricas
x = cos t + t sen t, y = sen t – t cos t, t > 0
do ponto P(x, y) para a involuta
Passo 1
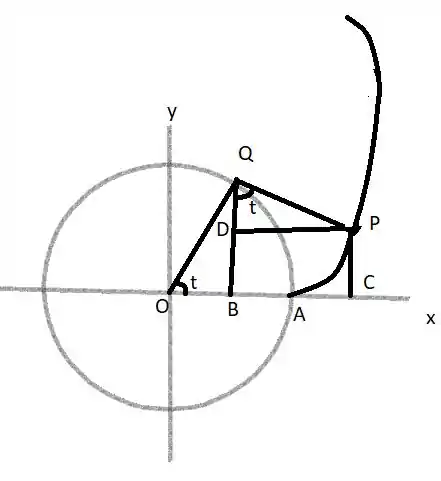Fala minha galera querida!! Vamos desenhar para nos direcionar:
O ponto é está em (1,0), o ponto P está em (x,y) e os ângulos QOB e são iguais, além de que PQ tem o mesmo comprimento do arco AQ, isto é, t.
Passo 2
Da figura tiramos que x = OB + BC = OB + DP, ou seja, . Não entendeu? Olha só, lembrando que a hipotenusa de QOB é 1 e de PQD é t:
e
De maneira semelhante, descobrimos o y,
e
Esta demonstrado as equações paramétricas.
Bora pro próximo.
Resposta
Demonstração.