Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.Revisão - Ex. 78
Um reservatório tem 80 m de comprimento e sua secção transversal é um trapézio isósceles com lados iguais de 10m, uma base superior de 17 m e uma base inferior de 5m. Quando a água tiver 5m de profundidade, ache a taxa segundo a qual estará escoando, se o nível de água estiver abaixando a uma taxa de 0,1 m/h
Passo 1
Bom, a questão nos pede a taxa a qual a água escoa, então precisaremos calcular o volume do trapézio, na imagem abaixo está a secção transversal dele:
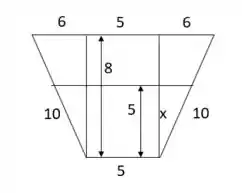
Pelo teorema de Pitágoras, podemos encontrar a profundidade máxima do trapézio (que já está na imagem):
Passo 2
Sendo x um nível qualquer de água no trapézio, podemos determinar qual é a área do trapézio como função de x. Para isso, precisamos descobrir o valor da linha horizontal do meio na imagem, ela também tem que ser função de x, pois como podemos ver, se x aumentar ou diminuir, o tamanho dessa linha vai mudar. Usaremos semelhança de triângulos:
Onde k é o lado do triângulo menor na linha horizontal
A linha horizontal então pode ser escrita somando cada parte que calculamos, 2k para os lados dos dois triângulos e 5 por causa da parte quadrada que não varia caso x mude:
E agora podemos escrever uma equação da área, como já sabemos a equação da linha, basta usarmos a equação de área do trapézio:
A base maior é a linha horizontal, a base menor já sabemos e a altura é x, ficamos com:
Passo 3
Para calcularmos o volume, precisamos multiplicar a área que calculamos pelo comprimento do reservatório:
Passo 4
Como o enunciado pede a taxa de água que escoa, vamos precisar derivar V em relação ao tempo:
O enunciado também nos dá a taxa de quanto o nível de água está baixando, que é , logo x depende de t. Então podemos resolver a derivada acima:
Passo 5
Substituindo e , ficamos com:
Então quando a água está em 5 metros de profundidade, a taxa de escoamento é de