Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 29
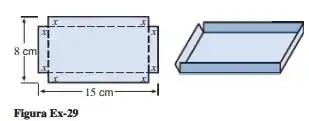
Conforme mostra a figura abaixo, uma caixa aberta deve ser construída de uma folha retangular de metal com 8 por 15 cm, cortando fora quadrados com lados de comprimento x de cada canto e dobrando os lados.
(a) Expresse o volume V como uma função de x.
(b) Encontre o domínio de V.
(c) Esboce o gráfico dafunção V obtida em (a) e estime a imagem dessa função.
(d) Com palavras, descreva como o volume V da caixa varia com x e discuta como poderiam ser construídas caixas com volume máximo.
Passo 1
(a) Show, temos que calcular o volume dessa caixa né? Deixando em função de . O volume pode ser calculado da forma clássica:
Ou seja, área da base multiplicada pela altura.
Como vemos na figura do problema, a base vai ser o retângulo pontilhado e a altura será , pois é onde terá a dobra.
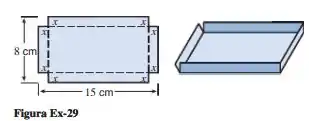
Como a base é um retângulo de dimensões e (são as dimensões do retângulo pontilhado, em que se tira de cada lado) sua área será:
E já vimos que a altura vale . Com isso, o volume será:
E será dado em , pois estaria em centímetros e a área da base, em centímetros quadrados.
Passo 2
(b) O domínio é o conjunto dos valores de .
Cara, só que é uma medida de comprimento, então ela não pode ser negativa! Além disso, não podemos cortar quadrados com lados maiores do que 4 cm, isso porque o menor dos lados tem 8 cm e são cortados dois quadrados né?
Dessa forma, os valores de no domínio devem estar entre e 4.
Prontinho, esse é o nosso domínio: .
Passo 3
(c) Para plotar o gráfico, temos que lembrar que não temos volume negativo! Então, só vamos pegar valores positivos do gráfico de . O gráfico dessa função é:
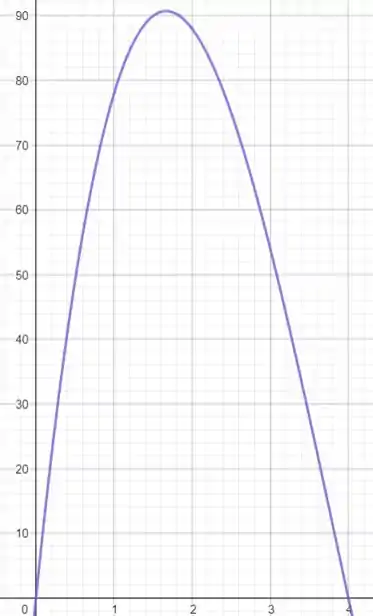
Olhando para o gráfico, podemos estimar que o valor máximo da função é mais ou menos em .
Como a imagem é o conjunto dos valores de , temos que a imagem será, aproximadamente:
Passo 4
(d) O gráfico nos mostra que a caixa com volume máximo ocorre para um valor de entre e e que o volume máximo é de aproximadamente . Além disso, o volume decresce a zero quando se aproxima de ou .
Resposta
(a)
(b)
(c)
(d) O gráfico nos mostra que a caixa com volume máximo ocorre para um valor de entre e e que o volume máximo é de aproximadamente . Além disso, o volume decresce a zero quando se aproxima de ou 4.