Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.Exercícios práticos - Ex. 21
Determine (a) o domínio e (b) a imagem de
Passo 1
E aí! Vou lembrar você de umas coisinhas:
Domínio de uma função: é onde o tá definido, com ou sem restrições
Imagem de uma função: são todos os que a função vai levar
Beleza? Vamos lá!
Passo 2
- Vamos olhar pra nossa função e ver se tem alguma restrição. Opa! A raiz quadrada nunca pode ser negativa, né? Então o que tá dentro não pode ser negativo
A gente quer onde a função é maior ou igual a zero. Olha só o gráfico dela:
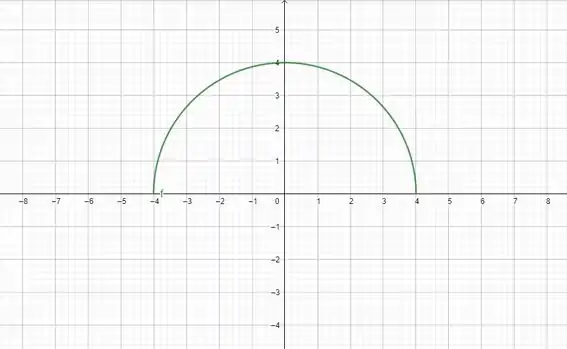
Ela é maior ou igual a zero de -4 a 4 (podendo ser -4 e 4).
Passo 3
(b) Agora, temos que ver o intervalo em que essa função vai levar. Olhando pro gráfico ali em cima, nós vemos que o vai só de 0 até 4.
Resposta
Exercícios de Livros Relacionados
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = x 2 + 1 5 0 ⋅ c o s ( 100 x )
Faça o gráfico da função f x = s e n 2 x + c o s ( 3 x )
Faça o gráfico da função f x = s e n 3 x
Faça o gráfico para dois períodos da função f x = 3 c o t g x 2 + 1
Faça o gráfico das funções f x = x / 2 e g x = 1 + ( 4 / x ) juntas para identificar os valores de x para os quais x 21 + 4 x Confirme algebricamente sua resposta no item ( a )