Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 - Ex. 26
Expresse o comprimento da corda de um círculo com raio de 10 cm como função do ângulo central (veja a figura abaixo).
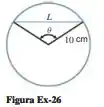
Passo 1
Bom, então, temos que achar alguma relação entre o ângulo e o comprimento .
O que temos na imagem que possa nos ajudar? Cara, se você olhar bem a imagem, você vai ver que temos um triângulo:
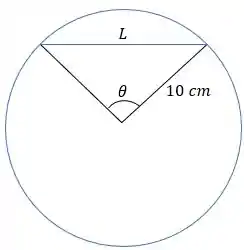
Esse triângulo com , e os de raio da circunferência.
E se liga, eu vi o triângulo e pensei logo num triângulo retângulo, para poder usar as relações de seno e cosseno nele. Dessa forma, relacionaria um ângulo com os lados do triângulo. Mas, infelizmente, não temos esse triângulo retângulo ali, AINDA.
Como podemos fazer ele aparecer? Bom, precisamos de um ângulo reto, certo? Podemos pegar a distância desde a metade de até o centro da circunferência! E como o está no centro da circunferência, dividiríamos ele pela metade, fazendo isso. Ficaria assim ó:
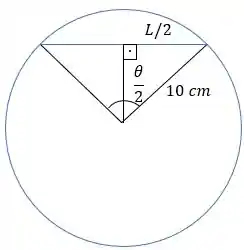
Opa, dessa forma, matamos o que precisávamos! Agora, temos nosso triângulo retângulo aí!
Passo 2
Então, agora, podemos usar o seno do , pois conhecemos o cateto oposto a ele () e a hipotenusa ():
Como queremos achar o em função do , só precisamos isolar ele nesse equação:
Prontinho!! É só isso.