Conforme mostra a figura a seguir, suponha que um barco entre em um rio no ponto e mantenha sua direção voltada para a origem. Como resultado da forte corrente, ele segue a trajetória onde e estão em quilômetros.
(a) Faça o gráfico da trajetória seguida pelo barco.
(b) O barco pode atingir a origem? Se não, discuta seu destino e descubra quão próximo estará dela.
Passo 1
(a) Tudo que a gente precisa fazer é usar um CAS para esboçar o gráfico de:
Como ele parte do ponto , nosso gráfico começa dele. Vamos usar o Wolfram Mathematica para fazer a trajetória. Fica assim:
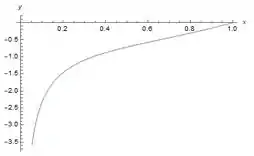
Passo 2
(b) Ele quer saber se o barco chega no ponto . Vemos pelo gráfico que isso não acontece. O barco é arrastado pela corrente para longe da origem, em direção ao sentido negativo de .
Repara também que a trajetória não está definida no ponto , então realmente nosso barquinho não passa aí.
Passo 3
Para achar o quão próximo nosso barco consegue chegar da origem, a gente precisa descobrir a menor distância entre o ponto e a nossa trajetória:
Ou seja, a gente vai minimizar a distância entre dois pontos. A fórmula da distância é:
Substituindo nossos dados, achamos uma função:
Passo 4
Agora a gente pode usar o CAS para achar o valor mínimo dessa função. Fica assim:
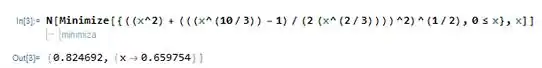
Vemos que o mais próximo que o barco chega da origem é a dela. E isso acontece quando .
Resposta
(a) 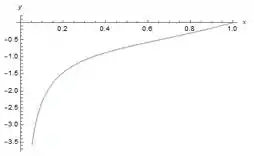
(b) Não. Ele chega a da origem e depois segue para baixo.