Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 67

Suponha que a função posição de uma partícula em movimento retilíneo seja dada pela fórmula

s t = t 2 + 1 t 4 + 1 ,     t ≥ 0

(a) Use um CAS para encontrar fórmulas simplificadas para a velocidade v ( t ) e para a aceleração a ( t ) .

(b) Faça os gráficos das curvas posição, velocidade e aceleração versus tempo.

(c) Use o gráfico apropriado para fazer uma estimativa do instante em que a partícula está mais longe da origem e sua distância até a origem nesse instante.

(d) Use o gráfico apropriado para fazer uma estimativa do intervalo de tempo durante o qual a partícula se move na direção positiva.

(e) Use os gráficos apropriados para fazer estimativas dos intervalos de tempo durante os quais a partícula está aumentando sua velocidade e dos intervalos de tempo durante os quais está diminuindo.

(f) Use o gráfico apropriado para fazer uma estimativa da velocidade máxima da partícula e do instante em que ela ocorre.

Passo 1

(a) Para fazer essa a gente precisa lembrar que:

v t = s ' t ,     a t = s ' ' ( t )

Então precisamos usar o CAS para calcular essas derivadas e simplificar o resultado. Usando o Wolfram Mathematica, fica assim:

Assim, a velocidade e a aceleração ficam com essa carinha:

v t = s ' t = - 2 - t + 2 t 3 + t 5 1 + t 4 2

a t = a ' ' t = 2 1 - 6 t 2 - 12 t 4 + 10 t 6 + 3 t 8 1 + t 4 3

Passo 2

(b) Vamos usar o CAS para fazer o gráfico das curvas que ele pediu. É só esboçar as funções que a gente já tem.

A função posição s ( t ) fica assim:

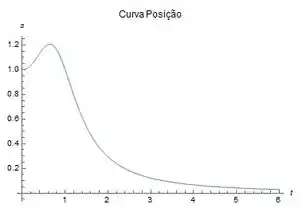
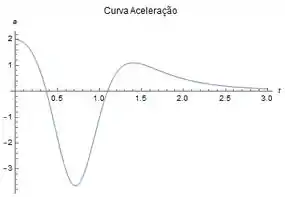
E essas são as curvas velocidade v ( t ) e aceleração a ( t ) :

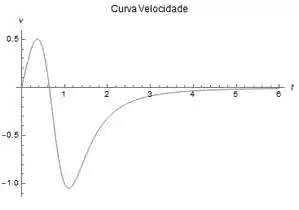
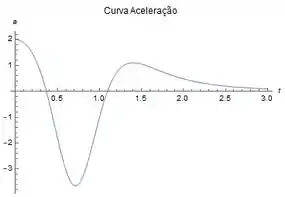
Passo 3

(c) Para achar o tempo em que a partícula está mais distante da origem, podemos olhar o gráfico de s ( t ) , e ver o instante onde essa função assume o maior valor.

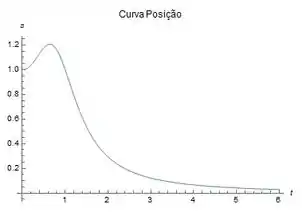
Usando o comando de coordenadas do CAS, a gente vê que isso acontece em:

t ≈ 0,64 ,     s t ≈ 1,20  

O valor da distância até a origem é o próprio valor da função posição nesse instante, que é 1,2 . Já que nosso referencial de s ( t ) é em relação à origem.

Passo 4

(d) Para saber o intervalo de tempo em que a partícula andou na direção positiva, podemos em olhar o intervalo onde a função posição cresceu. E isso é o mesmo que o olhar o intervalo onde:

s ' t = v t > 0

Olhando então no gráfico de v ( t ) ,

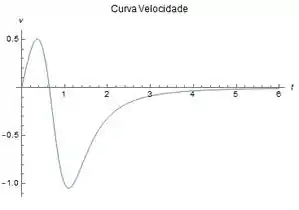
Vemos que ela assume valores positivos no intervalo:

0 < t < 0,64

Passo 5

(e) Como a gente quer os intervalos onde a função v ( t ) cresce e decresce, podemos olhar onde a sua derivada v ' t = a ( t ) , assume valores positivos e negativos.

Olhando o gráfico:

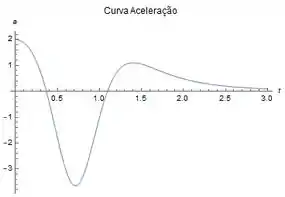
Vemos que a função a ( t ) é positiva em 0 < t < 0,36 e 1,1 < t . Logo a função velocidade cresce nesses intervalos.

E vemos que a ( t ) é negativa em 0,36 < t < 1,1 , logo nesse intervalo a velocidade decresce.

Passo 6

(f) Podemos usar o gráfico da velocidade para ver onde ela alcança o maior valor em módulo. Isso acontece ou no máximo ou no mínimo absoluto.

Olhando no gráfico, vemos que o valor máximo de | v t | acontece no mínimo absoluto, onde:

t ≈ 1,1 ∴ v t m á x = 1,05

Resposta

(a) v t = - 2 - t + 2 t 3 + t 5 1 + t 4 2 , a t = 2 1 - 6 t 2 - 12 t 4 + 10 t 6 + 3 t 8 1 + t 4 3

(b)

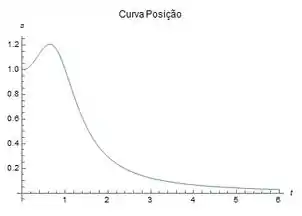
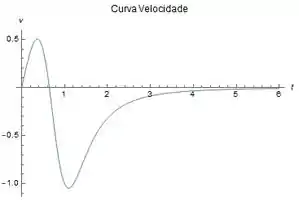
(c)   t ≈ 0,64 ,     s t ≈ 1,20 .   Distância máxima da origem é 1,2 .

(d)   0 < t < 0,64

(e) Cresce em 0 < t < 0,36 e 1,1 < t , e decresce em 0,36 < t < 1,1 .

(f) t ≈ 1,1 ∴ v t m á x = 1,05

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura Ex-69 mostra o gráfico do polinômio y = 0,1 x 5 x - 1 gerado em um computador usando uma janela de - 2 ; 2,5 × - 1 ,5 . Mostre que a escolha da escala vertical faz com que o computador perca
Uma caixa com base quadrada e sem tampa deve ser feita a partir de uma folha de metal, de forma que seu volume seja de 500c m 3 . Sejam S a área da superfície da caixa e x o comprimento de um lado da
55-60. Usando a regra de L’Hôpital (Seção 3.6), podemos conferir que: lim x → + ∞ ⁡ ln ⁡ x x r = 0 ,lim x → + ∞ ⁡ x r ln ⁡ x = + ∞ ,lim x → 0 + ⁡ x r ln ⁡ x = 0 Com qualquer número real positivo r . N
Um lote retangular deve ser cercado de forma que a área interna seja de 400m 2 . Sejam L o comprimento da cerca necessária e x o comprimento de um lado do retângulo; mostre que L = 2 x + 800 x para x0
61. Considere a família de curvas y = x e - b x b0 .a) Use um recurso gráfico computacional para gerar alguns membros dessa família.b) Discuta o efeito da variação de b na forma do gráfico e a localiz