Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 37

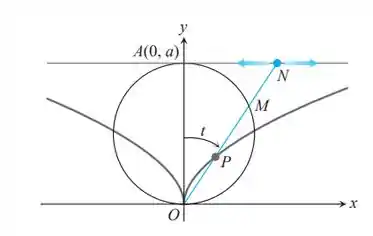
Conforme o ponto N se move ao longo da reta y = a na figura a seguir, P se move de forma que OP = MN. Encontre equações paramétricas para as coordenadas de P como funções do ângulo t que a reta ON faz com o eixo y positivo.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.

Vamos agora resolver os exercícios da seção 1 sobre determinação de equações paramétricas.

A partir do enunciado, desenhamos a linha AM na figura e observamos que o triângulo AMO tem um ângulo reto, pois é um ângulo inscrito que abrange o diâmetro de um círculo. Então:

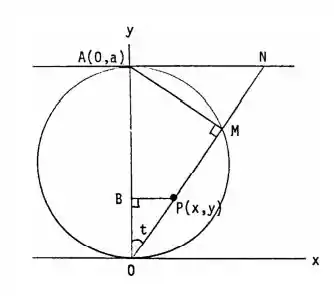
Daí, teremos que:

A N 2 = M N 2 + A M 2

Como:

O A = a

Temos que:

A N a = t g   t   e A M a = s e n   t

Como:

M N = O P

Teremos que:

O P 2 = A N 2 - A M 2 = a 2 t g 2   t - a 2 s e n 2   t

= > O P = a 2 t g 2   t - a 2 s e n 2   t = a s e n   t sec 2 ⁡ t - 1 = a   s e n 2   t cos ⁡ t

No triângulo BPO temos que:

x = O P   s e n   t = a   s e n 3   t cos ⁡ t = a   s e n 2   t   t g   t

E:

y = O P cos ⁡ t = a   s e n 2   t

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

x = a   s e n 2   t   t g   t

y = a   s e n 2   t

Exercícios de Livros Relacionados

Escreva uma equação polar de uma cônica com o foco na origem e com os dados fornecidos. E l i p s e , e x c e n t r i c i d a d e3 4, d i r e t r i zx = - 5
Hipocicloide - Quando um círculo rola dentro de um círculo fixo, qualquer ponto P na circunferência do círculo que rola descreve uma hipocicloide. Seja x 2 + y 2 = a 2 o círculo fixo, seja b o raio do
Encontre uma parametrização para o círculo x 2 + y 2 = 1 iniciando em (1, 0) e se movendo em sentido anti-horário até o ponto final (0, 1), com o ângulo u na figura a seguir como parâmetro.
Trocoides - Uma roda de raio a rola ao longo de uma reta horizontal sem deslizar. Encontre equações paramétricas para a curva traçada por um ponto P em um raio da roda a b unidades de seu centro. Como