Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 34

Encontre uma parametrização para o círculo x 2 + y 2 = 1 iniciando em (1, 0) e se movendo em sentido anti-horário até o ponto final (0, 1), com o ângulo u na figura a seguir como parâmetro.

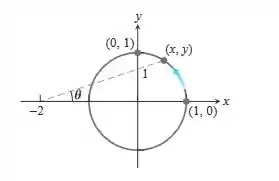
Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Da figura do enunciado, podemos escrever

tan ⁡ θ = y x + 2

Com isso, nós temos que

y = x + 2 tan ⁡ θ   1

Usando a equação (1) para substituir y = tan ⁡ θ em x 2 + y 2 = 1 , com isso,

x 2 + x + 2 2 tan 2 ⁡ θ = 1

Desenvolvendo os termos,

x 2 + x 2 + 4 x + 4 tan 2 ⁡ θ = 1

Um pouco mais...

x 2 1 + tan 2 ⁡ θ + 4 x tan ⁡ θ + 4 tan 2 ⁡ θ - 1 = 0

Tendo que 1 + tan 2 ⁡ θ = sec 2 ⁡ θ , logo,

x 2 sec 2 ⁡ θ + 4 x tan ⁡ θ + 4 tan 2 ⁡ θ - 1 = 0

Passo 2

Usando a fórmula quadrática para resolver a equação do 2° grau

x = - 4 tan ⁡ θ ± 4 tan ⁡ θ 2 - 4 sec 2 ⁡ θ 4 tan 2 ⁡ θ - 1 2 sec 2 ⁡ θ

Simplificando as coisas,

x = - 4 tan ⁡ θ ± 4 - 12 tan 2 ⁡ θ 2 sec 2 ⁡ θ = - 4 tan ⁡ θ ± 2 1 - 3 tan 2 ⁡ θ 2 sec 2 ⁡ θ

Como x é sempre positivo, rejeitamos a solução negativa

x = - 2 tan ⁡ θ + 1 - 3 tan 2 ⁡ θ sec 2 ⁡ θ

Passo 3

Substituindo esta expressão para x na equação (1), nós temos que

y = x + 2 tan ⁡ θ = - 2 tan ⁡ θ + 1 - 3 tan 2 ⁡ θ sec 2 ⁡ θ + 2 tan ⁡ θ

Para encontrar o valor máximo de θ , substitua x = 0 , y = 1 na Equação 1

1 = 0 + 2 tan ⁡ θ

Com isso, nós temos que

tan ⁡ θ = 1 2

Fazendo o arco tangente para encontrar o ângulo, obtemos que

θ = arctan ⁡ 1 2

Resposta

x = - 2 tan ⁡ θ + 1 - 3 tan 2 ⁡ θ sec 2 ⁡ θ ,   y = - 2 tan ⁡ θ + 1 - 3 tan 2 ⁡ θ sec 2 ⁡ θ + 2 tan ⁡ θ ,     0 ≤ θ ≤ arctan ⁡ 1 2

Exercícios de Livros Relacionados

Encontre uma equação em coordenadas polares para a curva:Encontre o comprimento da curva de t = 0 a t = 2 π .
Os Exercícios 19-22 fornecem as excentricidades das seções cônicas com um foco na origem do plano de coordenadas polares, com a diretriz para aquele foco. Encontre uma equação polar para cada seção cô
Os Exercícios 19-22 fornecem as excentricidades das seções cônicas com um foco na origem do plano de coordenadas polares, com a diretriz para aquele foco. Encontre uma equação polar para cada seção cô
Epicicloides. Quando um círculo gira externamente ao longo da circunferência de um segundo círculo fixo, qualquer ponto P na circunferência do círculo que gira descreve uma epicicloide, conforme mostr
Desenhe os gráficos dos conjuntos de pontos cujas coordenadas polares satisfaçam as equações e desigualdades nos Exercícios 11-26. π 4 ≤ θ ≤ 3 π 4 , 0 ≤ r ≤ 1