Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.7 - Ex. 10

Considere uma corda elástica de comprimento L. A extremidade x = 0 é mantida fixa, enquanto

a extremidade x = L está solta; assim, as condições de contorno são u(0, t) = 0 e u x ( L , t ) = 0 . A corda é colocada em movimento, sem velocidade inicial, a partir da posição inicial u(x, 0)=f(x), em que:

f ( x ) = 1 ,   L 2 - 1 < x < L 2 + 1 ( L > 2 )

  1. Calcule o deslocamento u(x, t).
  2. Com L = 10 e a = 1 , faça o gráfico de u em função de x para 0 ≤ x ≤ 10 e para diversos valores de t. Preste atenção especial aos valores de t entre 3 e 7. Note como a perturbação inicial é refletida em cada extremidade da corda.
  3. Com L=10 e a=1, faça o gráfico de u em função de t para diversos valores de x.
  4. Construa uma animação da solução no tempo durante pelo menos um período.
  5. Descreva o movimento da corda em poucas frases.

Passo 1

Letra a:

Temos a seguinte equação:

u ( x , t ) = ∑ n = 1 ∞ c n s i n n π x L c o s n π a t L

Daí, queremos achar o c n :

c n = 2 L ∫ 0 L f ( x ) s i n n π x L d x

Resolvendo, chegamos em:

c n = - 8 ( 2 n - 1 ) π s i n ( 2 n - 1 ) π 4 s i n ( 2 n - 1 ) π 2 L

Colocando na fórmula, chegamos em:

u ( x , t ) =   - 8 π ∑ n = 1 ∞ 1 2 n - 1 s i n ( 2 n - 1 ) π 4 s i n ( 2 n - 1 ) π 2 L . . . s i n ( 2 n - 1 ) π x 2 L c o s ( 2 n - 1 ) π a t 2 L

Passo 2

Na letra b:

Para L = 10   e   a = 1 , temos u ( x , t ) =   - 8 π ∑ n = 1 ∞ 1 2 n - 1 s i n ( 2 n - 1 ) π 4 s i n ( 2 n - 1 ) π 20 . . . s i n ( 2 n - 1 ) π x 20 c o s ( 2 n - 1 ) π t 20

Segue o gráfico de u ( x , t ) por x para vários valores de t:

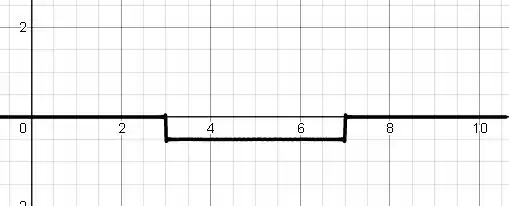
Passo 3

Letra c:

E agora, segue o gráfico de u ( x , t ) por t para vários valores de x :

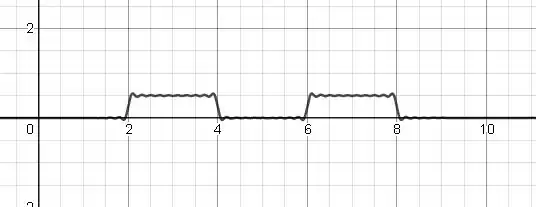
Passo 4

Letra d:

Para a animação, utilizar algum programa para gráficos animados.

Passo 5

Letra e:

As ondas são quadradas e primeiro elas passam em cima da linha numérica e depois abaixo.

Resposta

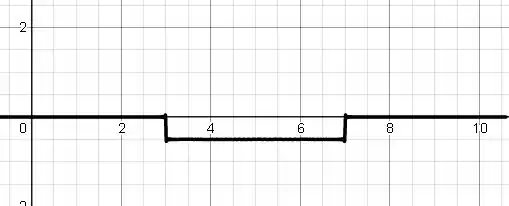
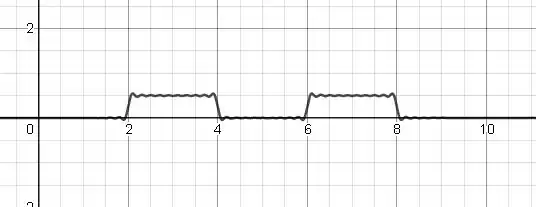
  1. u ( x , t ) =   - 8 π ∑ n = 1 ∞ 1 2 n - 1 s i n ( 2 n - 1 ) π 4 s i n ( 2 n - 1 ) π 2 L . . . s i n ( 2 n - 1 ) π x 2 L c o s ( 2 n - 1 ) π a t 2 L
  4. Para a animação, utilizar algum programa para gráficos animados.
  5. As ondas são quadradas e primeiro elas passam em cima da linha numérica e depois abaixo.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a equação de onda a 2 u x x = u t t pode ser reduzida à forma u x h = 0 pela mudança de variáveis ζ = x - a t ,η = x + a t Mostre que u(x, t) pode ser escrita como u ( x , t ) = ϕ ( x - a t
Considere uma corda elástica de comprimento L cujas extremidades são mantidas fixas. A corda écolocada em movimento a partir da sua posição de equilíbrio, com velocidade inicial ut(x, 0) = g(x). Em ca
Considere a equação de onda a 2 u x x = u t t em um meio unidimensional infinito, sujeita às condições iniciais u ( x , 0 ) = f ( x ) ,u t ( x , 0 ) = 0 ,- ∞x∞ . Usando a forma da solução obtida no Pr
Considere a equação de onda modificada a - 2 t n + γ 2 y = u x x ,0xL ,t0i com codições iniciais u 0 . t = 0 ,u L ,t = 0 ,t0i i E condições inciais u x , 0 = f x ,u 1 x , 0 = 0 ,0xLi i i a) Mostre que