Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.4 - Ex. 21
Em cada um dos problemas de 15 a 22:
(a) Encontre a série de Fourier indicada para a função dada.
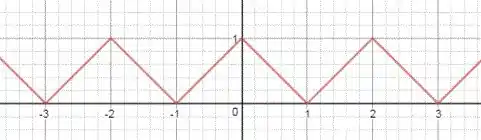
(b) Esboce o gráfico da função para a qual a série converge em um intervalo de três períodos.
21.
Compare com o Exemplo da seção 10.2.
Passo 1
(a) Fala galera!!!
A equação fornecida é a seguinte:
Queremos encontrar a série de Fourier para cossenos e esboçar o gráfico da função. Assim, precisamos encontrar os coeficientes e para a extensão par de período da função .
Passo 2
Agora, vamos calcular os coeficientes e . Para isso, podemos usar a seguinte relação fornecida no livro:
Em que a pode ser dada como uma série de Fourier da seguinte forma:
Para este caso, .
Passo 3
Podemos calcular da seguinte maneira:
Passo 4
Então, temos que é o seguinte:
Temos que sempre será , temos também que e .
Passo 5
Substituindo, os termos encontrados na relação fornecida no passo 1, temos que a série de Fourier de é a seguinte:
Vamos abrir a série da seguinte maneira:
Podemos perceber que quando é par o termo fica zero, assim, temos o seguinte:
Portanto, a solução necessária é:
Passo 6
(b) Podemos esboçar o gráfico da função da seguinte maneira:
