Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.2 - Ex. 21a

Considere o problema de Sturm-Liouville

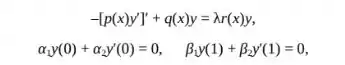
em que p, q e r satisfazem as condições enunciadas no texto.

Mostre que, se λ for um autovalor e se φ for uma autofunção associada, então

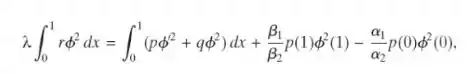
desde que α2 ≠ 0 e β2 ≠ 0. Como esse resultado tem que ser modificado, se α2 = 0 ou β2 = 0?

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para atribuirmos a definição do operador de Sturn-Liouville e testar a continuidade e positividade. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, nosso primeiro passo vai ser lembrar a definição da teoria de Sturn-Liouville

L ϕ = - p x ϕ ' x ' + q x ϕ x

Com isso, podemos aplicar a integral.

∫ L ϕ d ϕ =   ∫ - p x ϕ ' x ' ϕ d x + ∫ q x ϕ x   d x

Resolvendo essas primeira parcela da integral através do método da integração por partes, temos:

∫ - p x ϕ ' x ' ϕ d x = p 0 ϕ 0 ϕ ' 0 - p 1 ϕ 1 ϕ ' 1 + ∫ p ϕ ' 2 d x

Usando a condição de contorrno dada no enunciado, chegamos a

- p 0 ϕ 0 2 α 1 α 2 + p 1 ϕ 1 2 β 1 β 2 + ∫ p ϕ ' 2 + q ϕ 2 d x

Passo 3

Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!

Com a2 = 0

λ ∫ r ϕ ² d x   =   p 1 ϕ 1 2 β 1 β 2 + ∫ p ϕ ' 2 + q ϕ 2 d x

Com b2 = 0

λ ∫ r ϕ ² d x   =   - p 0 ϕ 0 2 α 1 α 2 + ∫ p ϕ ' 2 + q ϕ 2 d x

Resposta

Com a2 = 0

λ ∫ r ϕ ² d x   =   p 1 ϕ 1 2 β 1 β 2 + ∫ p ϕ ' 2 + q ϕ 2 d x

Com b2 = 0

λ ∫ r ϕ ² d x   =   - p 0 ϕ 0 2 α 1 α 2 + ∫ p ϕ ' 2 + q ϕ 2 d x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 14 a 18, determine se o problema de valor de contorno dado é autoadjunto.15. y ' ' + y = λ y , y 0 - y ' 1 = 0 ,y ' 0 - y 1 = 0
Em cada um dos problemas de 10 a 13, encontre os coeficientes da expansão em autofunções ∑ n = 1 ∞ a n ϕ n ( x ) da função dada, usando as autofunções normalizadas do problema 4.10. f x = 1 ,0 ≤ x ≤ 1
Em cada um dos problemas de 14 a 18, determine se o problema de valor de contorno dado é autoadjunto.18. ( 1 + x 2)y ' ' + 2 x y ' + y = 0 ,y ' ( 0 ) = 0 ,y ( 1 ) + 2 y ' ( 1 ) = 0
Em cada um dos problemas de 10 a 13, encontre os coeficientes da expansão em autofunções ∑ n = 1 ∞ a n ϕ n ( x ) da função dada, usando as autofunções normalizadas do problema 4.12. f x = 1 - x ,0 ≤ x
Em cada um dos problemas de 10 a 13, encontre os coeficientes da expansão em autofunções ∑ n = 1 ∞ a n ϕ n ( x ) da função dada, usando as autofunções normalizadas do problema 4.11. f x = x ,0 ≤ x ≤ 1