Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 11.4 - Ex. 2a
Considere o problema de valores de contorno.
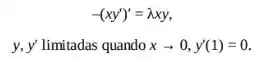
Mostre que λ0 = 0 é um autovalor desse problema com autofunção associada φ0(x) = 1. Se λ> 0, mostre, formalmente, que as autofunções são dadas por 
. É possível
mostrar que existe uma sequência infinita de tais raízes.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos as deformações verticais de uma barra em suas condições de contorno. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser analisar a equação dada.
Usando a definição das condições de contorno, tiramos:
Passo 3
Pronto!! Agora é só fazermos umas matemágicas aí pra achar o resultado!!
Resposta
Exercícios de Livros Relacionados
O fluxo laminar de um fluido incompressível viscoso em um tubo longo com seção reta circular, simétrico em relação ao eixo e com gradiente de pressão axial constante, é conhecido como fluxo de Poiseui
Considere uma barra metálica horizontal de comprimento L sujeita a uma carga vertical f ( x ) por unidade de comprimento. O deslocamento vertical resultante y ( x ) na barra satisfaz a equação diferen
Para cada uma das condições de contorno a seguir, encontre o menor autovalor (a força de deformação) de y ^(4) + λy′′ = 0 e encontre também a autofunção associada (a forma da coluna deformada).
Substâncias dissolvidas em um aquífero são transportadas por dois mecanismos separados. O processo pelo qual um soluto é transportado pelo grande movimento do fluxo da água subterrânea é chamado de ad
Considere o problema.Note que λ aparece como um coeficiente de y′, além do próprio y. É possível estender a definição de problema autoadjunto para esse tipo de problema e mostrar que esse problema par