Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 64
64. Considere a família de curvas , onde é um número inteiro positivo.
a) Use um recurso gráfico para gerar alguns membros dessa família.
b) Discuta o efeito de variar no formato do gráfico e discuta tanto a localização dos extremos relativos como dos pontos de inflexão.
Passo 1
a) A função que nos foi dada é a seguinte:
Gerar alguns membros dessa família é adotar alguns valores de , então:
Para :
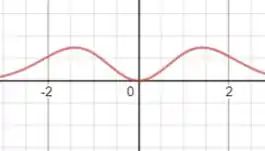
Para :
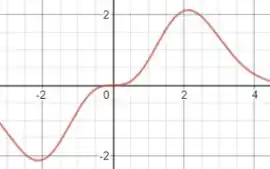
Para :
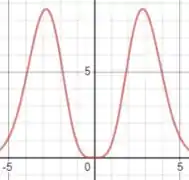
Note que a cada valor de a função deforma completamente. No entanto, essa é uma análise visual, então vamos calcular os extremos e os pontos de inflexão para termos um argumento mais profundo sobre o significado de na função.
Passo 2
b) Vamos derivar nossa função para encontrar os pontos críticos, se liga:
Igualando a zero, teremos:
A única forma disso dar zero é se:
Ou se:
Como está no numerador, o que conseguimos tirar de informação é que quanto mais aumentarmos , mais a função vai “esticar”, porque o valor de será maior, ou seja, mais distante da origem do gráfico. Essa análise vale tanto para a raíz positiva quanto pra negativa.
Passo 3
Quanto aos pontos de inflexão, temos:
Igualando a zero, teremos:
A única forma disso dar zero é se:
Ou seja, temos 4 pontos de inflexão!
E essa é a nossa resolução, galera!
Resposta
Ei, a resposta está no passo a passo :)