Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 68
Uma caixa com base quadrada e sem tampa deve ser feita a partir de uma folha de metal, de forma que seu volume seja de . Sejam a área da superfície da caixa e o comprimento de um lado da base quadrada. Mostre que para e esboce o gráfico de versus para .
Passo 1
Então pessoal, o volume de uma caixa quadrada é dado pelo produto entre a área da base a altura da caixa. Como o volume tem que ser de , então:
No qual a área da base é e a altura é , ok? Show! Ademais, sabemos que a área da superfície total da caixa é:
Oxe, da onde surgiu esse ? É que cada área lateral da caixa vale , e como são 4 lados, logo é a área de toda a caixa e é a área da base da mesma. Isolando da primeira equação, teremos:
Substituindo na segunda equação:
Assim como queríamos demonstrar!
Passo 2
Para esboçarmos o gráfico de versus temos que determinar os pontos críticos da função , para podermos encontrar os extremos relativos e os pontos de inflexão (se existirem). Derivando teremos:
Igualando nossa derivada a zero:
A única forma disso dar zero é se:
Beleza, descobrimos que é um ponto crítico. Se adotarmos valores de menores que e depois valores maiores do que notaremos que a derivada passa de negativa para positiva, o que indica um ponto de mínimo.
Passo 3
Por fim, vamos ver se a função apresenta pontos de inflexão:
A única forma disso dar zero é se:
O que resultará em uma raíz negativa, que não é um valor aceitável, uma vez que . Logo, não temos pontos de inflexão, o que facilita nosso esboço! Dessa forma, teremos um gráfico parecido com:
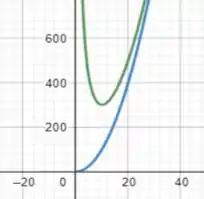
No qual a função em azul é a parábola , que é nosso limite oblíquo! E está aí nossa resolução, galera!
Resposta
Ei, a resposta está no passo a passo :)